Theorem dvmulxxbr 14169

Description: The product rule for derivatives at a point. For the (simpler but more limited) function version, see dvmulxx 14171. (Contributed by Mario Carneiro, 9-Aug-2014.) (Revised by Jim Kingdon, 1-Dec-2023.)

Hypotheses

Ref	Expression
dvadd.f	|- ( ph -> F : X --> CC )
dvadd.x	|- ( ph -> X C_ S )
dvaddxx.g	|- ( ph -> G : X --> CC )
dvaddbr.s	|- ( ph -> S C_ CC )
dvadd.bf	|- ( ph -> C ( S _D F ) K )
dvadd.bg	|- ( ph -> C ( S _D G ) L )
dvaddcntop.j	|- J = ( MetOpen ` ( abs o. - ) )

Assertion

Ref	Expression
dvmulxxbr	|- ( ph -> C ( S _D ( F oF x. G ) ) ( ( K x. ( G ` C ) ) + ( L x. ( F ` C ) ) ) )

Proof of Theorem dvmulxxbr

Dummy variables y z x w are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		dvadd.bf	. . . 4 |- ( ph -> C ( S _D F ) K )
2		eqid 2177	. . . . 5 |- ( J ↾t S ) = ( J ↾t S )
3		dvaddcntop.j	. . . . 5 |- J = ( MetOpen ` ( abs o. - ) )
4		eqid 2177	. . . . 5 |- ( z e. { w e. X | w # C } |-> ( ( ( F ` z ) - ( F ` C ) ) / ( z - C ) ) ) = ( z e. { w e. X | w # C } |-> ( ( ( F ` z ) - ( F ` C ) ) / ( z - C ) ) )
5		dvaddbr.s	. . . . 5 |- ( ph -> S C_ CC )
6		dvadd.f	. . . . 5 |- ( ph -> F : X --> CC )
7		dvadd.x	. . . . 5 |- ( ph -> X C_ S )
8	2, 3, 4, 5, 6, 7	eldvap 14154	. . . 4 |- ( ph -> ( C ( S _D F ) K <-> ( C e. ( ( int ` ( J ↾t S ) ) ` X ) /\ K e. ( ( z e. { w e. X | w # C } |-> ( ( ( F ` z ) - ( F ` C ) ) / ( z - C ) ) ) lim CC C ) ) ) )
9	1, 8	mpbid 147	. . 3 |- ( ph -> ( C e. ( ( int ` ( J ↾t S ) ) ` X ) /\ K e. ( ( z e. { w e. X | w # C } |-> ( ( ( F ` z ) - ( F ` C ) ) / ( z - C ) ) ) lim CC C ) ) )
10	9	simpld 112	. 2 |- ( ph -> C e. ( ( int ` ( J ↾t S ) ) ` X ) )
11	7, 5	sstrd 3166	. . . . . 6 |- ( ph -> X C_ CC )
12	3	cntoptopon 14035	. . . . . . . . . 10 |- J e. (TopOn ` CC )
13		resttopon 13674	. . . . . . . . . 10 |- ( ( J e. (TopOn ` CC ) /\ S C_ CC ) -> ( J ↾t S ) e. (TopOn ` S ) )
14	12, 5, 13	sylancr 414	. . . . . . . . 9 |- ( ph -> ( J ↾t S ) e. (TopOn ` S ) )
15		topontop 13517	. . . . . . . . 9 |- ( ( J ↾t S ) e. (TopOn ` S ) -> ( J ↾t S ) e. Top )
16	14, 15	syl 14	. . . . . . . 8 |- ( ph -> ( J ↾t S ) e. Top )
17		toponuni 13518	. . . . . . . . . 10 |- ( ( J ↾t S ) e. (TopOn ` S ) -> S = U. ( J ↾t S ) )
18	14, 17	syl 14	. . . . . . . . 9 |- ( ph -> S = U. ( J ↾t S ) )
19	7, 18	sseqtrd 3194	. . . . . . . 8 |- ( ph -> X C_ U. ( J ↾t S ) )
20		eqid 2177	. . . . . . . . 9 |- U. ( J ↾t S ) = U. ( J ↾t S )
21	20	ntrss2 13624	. . . . . . . 8 |- ( ( ( J ↾t S ) e. Top /\ X C_ U. ( J ↾t S ) ) -> ( ( int ` ( J ↾t S ) ) ` X ) C_ X )
22	16, 19, 21	syl2anc 411	. . . . . . 7 |- ( ph -> ( ( int ` ( J ↾t S ) ) ` X ) C_ X )
23	22, 10	sseldd 3157	. . . . . 6 |- ( ph -> C e. X )
24	6, 11, 23	dvlemap 14152	. . . . 5 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( ( F ` z ) - ( F ` C ) ) / ( z - C ) ) e. CC )
25		dvaddxx.g	. . . . . . 7 |- ( ph -> G : X --> CC )
26	25	adantr 276	. . . . . 6 |- ( ( ph /\ z e. { w e. X | w # C } ) -> G : X --> CC )
27		elrabi 2891	. . . . . . 7 |- ( z e. { w e. X | w # C } -> z e. X )
28	27	adantl 277	. . . . . 6 |- ( ( ph /\ z e. { w e. X | w # C } ) -> z e. X )
29	26, 28	ffvelcdmd 5653	. . . . 5 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( G ` z ) e. CC )
30	24, 29	mulcld 7978	. . . 4 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( ( ( F ` z ) - ( F ` C ) ) / ( z - C ) ) x. ( G ` z ) ) e. CC )
31	25, 11, 23	dvlemap 14152	. . . . 5 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( ( G ` z ) - ( G ` C ) ) / ( z - C ) ) e. CC )
32	6, 23	ffvelcdmd 5653	. . . . . 6 |- ( ph -> ( F ` C ) e. CC )
33	32	adantr 276	. . . . 5 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( F ` C ) e. CC )
34	31, 33	mulcld 7978	. . . 4 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( ( ( G ` z ) - ( G ` C ) ) / ( z - C ) ) x. ( F ` C ) ) e. CC )
35		ssidd 3177	. . . 4 |- ( ph -> CC C_ CC )
36		txtopon 13765	. . . . . 6 |- ( ( J e. (TopOn ` CC ) /\ J e. (TopOn ` CC ) ) -> ( J tX J ) e. (TopOn ` ( CC X. CC ) ) )
37	12, 12, 36	mp2an 426	. . . . 5 |- ( J tX J ) e. (TopOn ` ( CC X. CC ) )
38	37	toponrestid 13524	. . . 4 |- ( J tX J ) = ( ( J tX J ) ↾t ( CC X. CC ) )
39	9	simprd 114	. . . . 5 |- ( ph -> K e. ( ( z e. { w e. X | w # C } |-> ( ( ( F ` z ) - ( F ` C ) ) / ( z - C ) ) ) lim CC C ) )
40		cnex 7935	. . . . . . . . . . . . 13 |- CC e. _V
41	40	a1i 9	. . . . . . . . . . . 12 |- ( ph -> CC e. _V )
42	41, 5	ssexd 4144	. . . . . . . . . . . 12 |- ( ph -> S e. _V )
43		elpm2r 6666	. . . . . . . . . . . 12 |- ( ( ( CC e. _V /\ S e. _V ) /\ ( G : X --> CC /\ X C_ S ) ) -> G e. ( CC ^pm S ) )
44	41, 42, 25, 7, 43	syl22anc 1239	. . . . . . . . . . 11 |- ( ph -> G e. ( CC ^pm S ) )
45		reldvg 14151	. . . . . . . . . . 11 |- ( ( S C_ CC /\ G e. ( CC ^pm S ) ) -> Rel ( S _D G ) )
46	5, 44, 45	syl2anc 411	. . . . . . . . . 10 |- ( ph -> Rel ( S _D G ) )
47		dvadd.bg	. . . . . . . . . 10 |- ( ph -> C ( S _D G ) L )
48		releldm 4863	. . . . . . . . . 10 |- ( ( Rel ( S _D G ) /\ C ( S _D G ) L ) -> C e. dom ( S _D G ) )
49	46, 47, 48	syl2anc 411	. . . . . . . . 9 |- ( ph -> C e. dom ( S _D G ) )
50		eqid 2177	. . . . . . . . . 10 |- ( J ↾t X ) = ( J ↾t X )
51	50, 3	dvcnp2cntop 14166	. . . . . . . . 9 |- ( ( ( S C_ CC /\ G : X --> CC /\ X C_ S ) /\ C e. dom ( S _D G ) ) -> G e. ( ( ( J ↾t X ) CnP J ) ` C ) )
52	5, 25, 7, 49, 51	syl31anc 1241	. . . . . . . 8 |- ( ph -> G e. ( ( ( J ↾t X ) CnP J ) ` C ) )
53	3, 50	cnplimccntop 14142	. . . . . . . . 9 |- ( ( X C_ CC /\ C e. X ) -> ( G e. ( ( ( J ↾t X ) CnP J ) ` C ) <-> ( G : X --> CC /\ ( G ` C ) e. ( G lim CC C ) ) ) )
54	11, 23, 53	syl2anc 411	. . . . . . . 8 |- ( ph -> ( G e. ( ( ( J ↾t X ) CnP J ) ` C ) <-> ( G : X --> CC /\ ( G ` C ) e. ( G lim CC C ) ) ) )
55	52, 54	mpbid 147	. . . . . . 7 |- ( ph -> ( G : X --> CC /\ ( G ` C ) e. ( G lim CC C ) ) )
56	55	simprd 114	. . . . . 6 |- ( ph -> ( G ` C ) e. ( G lim CC C ) )
57	25, 11	limcdifap 14134	. . . . . . 7 |- ( ph -> ( G lim CC C ) = ( ( G |` { w e. X | w # C } ) lim CC C ) )
58		ssrab2 3241	. . . . . . . . . 10 |- { w e. X | w # C } C_ X
59	58	a1i 9	. . . . . . . . 9 |- ( ph -> { w e. X | w # C } C_ X )
60	25, 59	feqresmpt 5571	. . . . . . . 8 |- ( ph -> ( G |` { w e. X | w # C } ) = ( z e. { w e. X | w # C } |-> ( G ` z ) ) )
61	60	oveq1d 5890	. . . . . . 7 |- ( ph -> ( ( G |` { w e. X | w # C } ) lim CC C ) = ( ( z e. { w e. X | w # C } |-> ( G ` z ) ) lim CC C ) )
62	57, 61	eqtrd 2210	. . . . . 6 |- ( ph -> ( G lim CC C ) = ( ( z e. { w e. X | w # C } |-> ( G ` z ) ) lim CC C ) )
63	56, 62	eleqtrd 2256	. . . . 5 |- ( ph -> ( G ` C ) e. ( ( z e. { w e. X | w # C } |-> ( G ` z ) ) lim CC C ) )
64	3	mulcncntop 14057	. . . . . 6 |- x. e. ( ( J tX J ) Cn J )
65	5, 6, 7	dvcl 14155	. . . . . . . 8 |- ( ( ph /\ C ( S _D F ) K ) -> K e. CC )
66	1, 65	mpdan 421	. . . . . . 7 |- ( ph -> K e. CC )
67	25, 23	ffvelcdmd 5653	. . . . . . 7 |- ( ph -> ( G ` C ) e. CC )
68	66, 67	opelxpd 4660	. . . . . 6 |- ( ph -> <. K , ( G ` C ) >. e. ( CC X. CC ) )
69	37	toponunii 13520	. . . . . . 7 |- ( CC X. CC ) = U. ( J tX J )
70	69	cncnpi 13731	. . . . . 6 |- ( ( x. e. ( ( J tX J ) Cn J ) /\ <. K , ( G ` C ) >. e. ( CC X. CC ) ) -> x. e. ( ( ( J tX J ) CnP J ) ` <. K , ( G ` C ) >. ) )
71	64, 68, 70	sylancr 414	. . . . 5 |- ( ph -> x. e. ( ( ( J tX J ) CnP J ) ` <. K , ( G ` C ) >. ) )
72	24, 29, 35, 35, 3, 38, 39, 63, 71	limccnp2cntop 14149	. . . 4 |- ( ph -> ( K x. ( G ` C ) ) e. ( ( z e. { w e. X | w # C } |-> ( ( ( ( F ` z ) - ( F ` C ) ) / ( z - C ) ) x. ( G ` z ) ) ) lim CC C ) )
73		eqid 2177	. . . . . . . 8 |- ( z e. { w e. X | w # C } |-> ( ( ( G ` z ) - ( G ` C ) ) / ( z - C ) ) ) = ( z e. { w e. X | w # C } |-> ( ( ( G ` z ) - ( G ` C ) ) / ( z - C ) ) )
74	2, 3, 73, 5, 25, 7	eldvap 14154	. . . . . . 7 |- ( ph -> ( C ( S _D G ) L <-> ( C e. ( ( int ` ( J ↾t S ) ) ` X ) /\ L e. ( ( z e. { w e. X | w # C } |-> ( ( ( G ` z ) - ( G ` C ) ) / ( z - C ) ) ) lim CC C ) ) ) )
75	47, 74	mpbid 147	. . . . . 6 |- ( ph -> ( C e. ( ( int ` ( J ↾t S ) ) ` X ) /\ L e. ( ( z e. { w e. X | w # C } |-> ( ( ( G ` z ) - ( G ` C ) ) / ( z - C ) ) ) lim CC C ) ) )
76	75	simprd 114	. . . . 5 |- ( ph -> L e. ( ( z e. { w e. X | w # C } |-> ( ( ( G ` z ) - ( G ` C ) ) / ( z - C ) ) ) lim CC C ) )
77		cncfmptc 14085	. . . . . . . 8 |- ( ( ( F ` C ) e. CC /\ X C_ CC /\ CC C_ CC ) -> ( z e. X |-> ( F ` C ) ) e. ( X -cn-> CC ) )
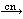78	32, 11, 35, 77	syl3anc 1238	. . . . . . 7 |- ( ph -> ( z e. X |-> ( F ` C ) ) e. ( X -cn-> CC ) )
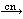79		eqidd 2178	. . . . . . 7 |- ( z = C -> ( F ` C ) = ( F ` C ) )
80	78, 23, 79	cnmptlimc 14146	. . . . . 6 |- ( ph -> ( F ` C ) e. ( ( z e. X |-> ( F ` C ) ) lim CC C ) )
81	32	adantr 276	. . . . . . . . 9 |- ( ( ph /\ z e. X ) -> ( F ` C ) e. CC )
82	81	fmpttd 5672	. . . . . . . 8 |- ( ph -> ( z e. X |-> ( F ` C ) ) : X --> CC )
83	82, 11	limcdifap 14134	. . . . . . 7 |- ( ph -> ( ( z e. X |-> ( F ` C ) ) lim CC C ) = ( ( ( z e. X |-> ( F ` C ) ) |` { w e. X | w # C } ) lim CC C ) )
84		resmpt 4956	. . . . . . . . 9 |- ( { w e. X | w # C } C_ X -> ( ( z e. X |-> ( F ` C ) ) |` { w e. X | w # C } ) = ( z e. { w e. X | w # C } |-> ( F ` C ) ) )
85	58, 84	mp1i 10	. . . . . . . 8 |- ( ph -> ( ( z e. X |-> ( F ` C ) ) |` { w e. X | w # C } ) = ( z e. { w e. X | w # C } |-> ( F ` C ) ) )
86	85	oveq1d 5890	. . . . . . 7 |- ( ph -> ( ( ( z e. X |-> ( F ` C ) ) |` { w e. X | w # C } ) lim CC C ) = ( ( z e. { w e. X | w # C } |-> ( F ` C ) ) lim CC C ) )
87	83, 86	eqtrd 2210	. . . . . 6 |- ( ph -> ( ( z e. X |-> ( F ` C ) ) lim CC C ) = ( ( z e. { w e. X | w # C } |-> ( F ` C ) ) lim CC C ) )
88	80, 87	eleqtrd 2256	. . . . 5 |- ( ph -> ( F ` C ) e. ( ( z e. { w e. X | w # C } |-> ( F ` C ) ) lim CC C ) )
89	5, 25, 7	dvcl 14155	. . . . . . . 8 |- ( ( ph /\ C ( S _D G ) L ) -> L e. CC )
90	47, 89	mpdan 421	. . . . . . 7 |- ( ph -> L e. CC )
91	90, 32	opelxpd 4660	. . . . . 6 |- ( ph -> <. L , ( F ` C ) >. e. ( CC X. CC ) )
92	69	cncnpi 13731	. . . . . 6 |- ( ( x. e. ( ( J tX J ) Cn J ) /\ <. L , ( F ` C ) >. e. ( CC X. CC ) ) -> x. e. ( ( ( J tX J ) CnP J ) ` <. L , ( F ` C ) >. ) )
93	64, 91, 92	sylancr 414	. . . . 5 |- ( ph -> x. e. ( ( ( J tX J ) CnP J ) ` <. L , ( F ` C ) >. ) )
94	31, 33, 35, 35, 3, 38, 76, 88, 93	limccnp2cntop 14149	. . . 4 |- ( ph -> ( L x. ( F ` C ) ) e. ( ( z e. { w e. X | w # C } |-> ( ( ( ( G ` z ) - ( G ` C ) ) / ( z - C ) ) x. ( F ` C ) ) ) lim CC C ) )
95	3	addcncntop 14055	. . . . 5 |- + e. ( ( J tX J ) Cn J )
96	66, 67	mulcld 7978	. . . . . 6 |- ( ph -> ( K x. ( G ` C ) ) e. CC )
97	90, 32	mulcld 7978	. . . . . 6 |- ( ph -> ( L x. ( F ` C ) ) e. CC )
98	96, 97	opelxpd 4660	. . . . 5 |- ( ph -> <. ( K x. ( G ` C ) ) , ( L x. ( F ` C ) ) >. e. ( CC X. CC ) )
99	69	cncnpi 13731	. . . . 5 |- ( ( + e. ( ( J tX J ) Cn J ) /\ <. ( K x. ( G ` C ) ) , ( L x. ( F ` C ) ) >. e. ( CC X. CC ) ) -> + e. ( ( ( J tX J ) CnP J ) ` <. ( K x. ( G ` C ) ) , ( L x. ( F ` C ) ) >. ) )
100	95, 98, 99	sylancr 414	. . . 4 |- ( ph -> + e. ( ( ( J tX J ) CnP J ) ` <. ( K x. ( G ` C ) ) , ( L x. ( F ` C ) ) >. ) )
101	30, 34, 35, 35, 3, 38, 72, 94, 100	limccnp2cntop 14149	. . 3 |- ( ph -> ( ( K x. ( G ` C ) ) + ( L x. ( F ` C ) ) ) e. ( ( z e. { w e. X | w # C } |-> ( ( ( ( ( F ` z ) - ( F ` C ) ) / ( z - C ) ) x. ( G ` z ) ) + ( ( ( ( G ` z ) - ( G ` C ) ) / ( z - C ) ) x. ( F ` C ) ) ) ) lim CC C ) )
102	6	adantr 276	. . . . . . . . . 10 |- ( ( ph /\ z e. { w e. X | w # C } ) -> F : X --> CC )
103	102, 28	ffvelcdmd 5653	. . . . . . . . 9 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( F ` z ) e. CC )
104	103, 33	subcld 8268	. . . . . . . 8 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( F ` z ) - ( F ` C ) ) e. CC )
105	104, 29	mulcld 7978	. . . . . . 7 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( ( F ` z ) - ( F ` C ) ) x. ( G ` z ) ) e. CC )
106	67	adantr 276	. . . . . . . . 9 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( G ` C ) e. CC )
107	29, 106	subcld 8268	. . . . . . . 8 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( G ` z ) - ( G ` C ) ) e. CC )
108	107, 33	mulcld 7978	. . . . . . 7 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( ( G ` z ) - ( G ` C ) ) x. ( F ` C ) ) e. CC )
109	11	adantr 276	. . . . . . . . 9 |- ( ( ph /\ z e. { w e. X | w # C } ) -> X C_ CC )
110	109, 28	sseldd 3157	. . . . . . . 8 |- ( ( ph /\ z e. { w e. X | w # C } ) -> z e. CC )
111	11, 23	sseldd 3157	. . . . . . . . 9 |- ( ph -> C e. CC )
112	111	adantr 276	. . . . . . . 8 |- ( ( ph /\ z e. { w e. X | w # C } ) -> C e. CC )
113	110, 112	subcld 8268	. . . . . . 7 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( z - C ) e. CC )
114		breq1 4007	. . . . . . . . . . 11 |- ( w = z -> ( w # C <-> z # C ) )
115	114	elrab 2894	. . . . . . . . . 10 |- ( z e. { w e. X | w # C } <-> ( z e. X /\ z # C ) )
116	115	simprbi 275	. . . . . . . . 9 |- ( z e. { w e. X | w # C } -> z # C )
117	116	adantl 277	. . . . . . . 8 |- ( ( ph /\ z e. { w e. X | w # C } ) -> z # C )
118	110, 112, 117	subap0d 8601	. . . . . . 7 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( z - C ) # 0 )
119	105, 108, 113, 118	divdirapd 8786	. . . . . 6 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( ( ( ( F ` z ) - ( F ` C ) ) x. ( G ` z ) ) + ( ( ( G ` z ) - ( G ` C ) ) x. ( F ` C ) ) ) / ( z - C ) ) = ( ( ( ( ( F ` z ) - ( F ` C ) ) x. ( G ` z ) ) / ( z - C ) ) + ( ( ( ( G ` z ) - ( G ` C ) ) x. ( F ` C ) ) / ( z - C ) ) ) )
120	103, 29	mulcld 7978	. . . . . . . . 9 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( F ` z ) x. ( G ` z ) ) e. CC )
121	33, 29	mulcld 7978	. . . . . . . . 9 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( F ` C ) x. ( G ` z ) ) e. CC )
122	33, 106	mulcld 7978	. . . . . . . . 9 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( F ` C ) x. ( G ` C ) ) e. CC )
123	120, 121, 122	npncand 8292	. . . . . . . 8 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( ( ( F ` z ) x. ( G ` z ) ) - ( ( F ` C ) x. ( G ` z ) ) ) + ( ( ( F ` C ) x. ( G ` z ) ) - ( ( F ` C ) x. ( G ` C ) ) ) ) = ( ( ( F ` z ) x. ( G ` z ) ) - ( ( F ` C ) x. ( G ` C ) ) ) )
124	103, 33, 29	subdird 8372	. . . . . . . . 9 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( ( F ` z ) - ( F ` C ) ) x. ( G ` z ) ) = ( ( ( F ` z ) x. ( G ` z ) ) - ( ( F ` C ) x. ( G ` z ) ) ) )
125	107, 33	mulcomd 7979	. . . . . . . . . 10 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( ( G ` z ) - ( G ` C ) ) x. ( F ` C ) ) = ( ( F ` C ) x. ( ( G ` z ) - ( G ` C ) ) ) )
126	33, 29, 106	subdid 8371	. . . . . . . . . 10 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( F ` C ) x. ( ( G ` z ) - ( G ` C ) ) ) = ( ( ( F ` C ) x. ( G ` z ) ) - ( ( F ` C ) x. ( G ` C ) ) ) )
127	125, 126	eqtrd 2210	. . . . . . . . 9 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( ( G ` z ) - ( G ` C ) ) x. ( F ` C ) ) = ( ( ( F ` C ) x. ( G ` z ) ) - ( ( F ` C ) x. ( G ` C ) ) ) )
128	124, 127	oveq12d 5893	. . . . . . . 8 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( ( ( F ` z ) - ( F ` C ) ) x. ( G ` z ) ) + ( ( ( G ` z ) - ( G ` C ) ) x. ( F ` C ) ) ) = ( ( ( ( F ` z ) x. ( G ` z ) ) - ( ( F ` C ) x. ( G ` z ) ) ) + ( ( ( F ` C ) x. ( G ` z ) ) - ( ( F ` C ) x. ( G ` C ) ) ) ) )
129	28, 28	elind 3321	. . . . . . . . . 10 |- ( ( ph /\ z e. { w e. X | w # C } ) -> z e. ( X i^i X ) )
130	6	ffnd 5367	. . . . . . . . . . . 12 |- ( ph -> F Fn X )
131	130	adantr 276	. . . . . . . . . . 11 |- ( ( ph /\ z e. { w e. X | w # C } ) -> F Fn X )
132	25	ffnd 5367	. . . . . . . . . . . 12 |- ( ph -> G Fn X )
133	132	adantr 276	. . . . . . . . . . 11 |- ( ( ph /\ z e. { w e. X | w # C } ) -> G Fn X )
134		ssexg 4143	. . . . . . . . . . . . 13 |- ( ( X C_ CC /\ CC e. _V ) -> X e. _V )
135	11, 40, 134	sylancl 413	. . . . . . . . . . . 12 |- ( ph -> X e. _V )
136	135	adantr 276	. . . . . . . . . . 11 |- ( ( ph /\ z e. { w e. X | w # C } ) -> X e. _V )
137		eqid 2177	. . . . . . . . . . 11 |- ( X i^i X ) = ( X i^i X )
138		eqidd 2178	. . . . . . . . . . 11 |- ( ( ( ph /\ z e. { w e. X | w # C } ) /\ z e. X ) -> ( F ` z ) = ( F ` z ) )
139		eqidd 2178	. . . . . . . . . . 11 |- ( ( ( ph /\ z e. { w e. X | w # C } ) /\ z e. X ) -> ( G ` z ) = ( G ` z ) )
140	120	adantr 276	. . . . . . . . . . 11 |- ( ( ( ph /\ z e. { w e. X | w # C } ) /\ z e. ( X i^i X ) ) -> ( ( F ` z ) x. ( G ` z ) ) e. CC )
141	131, 133, 136, 136, 137, 138, 139, 140	ofvalg 6092	. . . . . . . . . 10 |- ( ( ( ph /\ z e. { w e. X | w # C } ) /\ z e. ( X i^i X ) ) -> ( ( F oF x. G ) ` z ) = ( ( F ` z ) x. ( G ` z ) ) )
142	129, 141	mpdan 421	. . . . . . . . 9 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( F oF x. G ) ` z ) = ( ( F ` z ) x. ( G ` z ) ) )
143	23, 23	elind 3321	. . . . . . . . . 10 |- ( ph -> C e. ( X i^i X ) )
144		eqidd 2178	. . . . . . . . . . 11 |- ( ( ( ph /\ z e. { w e. X | w # C } ) /\ C e. X ) -> ( F ` C ) = ( F ` C ) )
145		eqidd 2178	. . . . . . . . . . 11 |- ( ( ( ph /\ z e. { w e. X | w # C } ) /\ C e. X ) -> ( G ` C ) = ( G ` C ) )
146	122	adantr 276	. . . . . . . . . . 11 |- ( ( ( ph /\ z e. { w e. X | w # C } ) /\ C e. ( X i^i X ) ) -> ( ( F ` C ) x. ( G ` C ) ) e. CC )
147	131, 133, 136, 136, 137, 144, 145, 146	ofvalg 6092	. . . . . . . . . 10 |- ( ( ( ph /\ z e. { w e. X | w # C } ) /\ C e. ( X i^i X ) ) -> ( ( F oF x. G ) ` C ) = ( ( F ` C ) x. ( G ` C ) ) )
148	143, 147	mpidan 423	. . . . . . . . 9 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( F oF x. G ) ` C ) = ( ( F ` C ) x. ( G ` C ) ) )
149	142, 148	oveq12d 5893	. . . . . . . 8 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( ( F oF x. G ) ` z ) - ( ( F oF x. G ) ` C ) ) = ( ( ( F ` z ) x. ( G ` z ) ) - ( ( F ` C ) x. ( G ` C ) ) ) )
150	123, 128, 149	3eqtr4d 2220	. . . . . . 7 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( ( ( F ` z ) - ( F ` C ) ) x. ( G ` z ) ) + ( ( ( G ` z ) - ( G ` C ) ) x. ( F ` C ) ) ) = ( ( ( F oF x. G ) ` z ) - ( ( F oF x. G ) ` C ) ) )
151	150	oveq1d 5890	. . . . . 6 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( ( ( ( F ` z ) - ( F ` C ) ) x. ( G ` z ) ) + ( ( ( G ` z ) - ( G ` C ) ) x. ( F ` C ) ) ) / ( z - C ) ) = ( ( ( ( F oF x. G ) ` z ) - ( ( F oF x. G ) ` C ) ) / ( z - C ) ) )
152	104, 29, 113, 118	div23apd 8785	. . . . . . 7 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( ( ( F ` z ) - ( F ` C ) ) x. ( G ` z ) ) / ( z - C ) ) = ( ( ( ( F ` z ) - ( F ` C ) ) / ( z - C ) ) x. ( G ` z ) ) )
153	107, 33, 113, 118	div23apd 8785	. . . . . . 7 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( ( ( G ` z ) - ( G ` C ) ) x. ( F ` C ) ) / ( z - C ) ) = ( ( ( ( G ` z ) - ( G ` C ) ) / ( z - C ) ) x. ( F ` C ) ) )
154	152, 153	oveq12d 5893	. . . . . 6 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( ( ( ( F ` z ) - ( F ` C ) ) x. ( G ` z ) ) / ( z - C ) ) + ( ( ( ( G ` z ) - ( G ` C ) ) x. ( F ` C ) ) / ( z - C ) ) ) = ( ( ( ( ( F ` z ) - ( F ` C ) ) / ( z - C ) ) x. ( G ` z ) ) + ( ( ( ( G ` z ) - ( G ` C ) ) / ( z - C ) ) x. ( F ` C ) ) ) )
155	119, 151, 154	3eqtr3d 2218	. . . . 5 |- ( ( ph /\ z e. { w e. X | w # C } ) -> ( ( ( ( F oF x. G ) ` z ) - ( ( F oF x. G ) ` C ) ) / ( z - C ) ) = ( ( ( ( ( F ` z ) - ( F ` C ) ) / ( z - C ) ) x. ( G ` z ) ) + ( ( ( ( G ` z ) - ( G ` C ) ) / ( z - C ) ) x. ( F ` C ) ) ) )
156	155	mpteq2dva 4094	. . . 4 |- ( ph -> ( z e. { w e. X | w # C } |-> ( ( ( ( F oF x. G ) ` z ) - ( ( F oF x. G ) ` C ) ) / ( z - C ) ) ) = ( z e. { w e. X | w # C } |-> ( ( ( ( ( F ` z ) - ( F ` C ) ) / ( z - C ) ) x. ( G ` z ) ) + ( ( ( ( G ` z ) - ( G ` C ) ) / ( z - C ) ) x. ( F ` C ) ) ) ) )
157	156	oveq1d 5890	. . 3 |- ( ph -> ( ( z e. { w e. X | w # C } |-> ( ( ( ( F oF x. G ) ` z ) - ( ( F oF x. G ) ` C ) ) / ( z - C ) ) ) lim CC C ) = ( ( z e. { w e. X | w # C } |-> ( ( ( ( ( F ` z ) - ( F ` C ) ) / ( z - C ) ) x. ( G ` z ) ) + ( ( ( ( G ` z ) - ( G ` C ) ) / ( z - C ) ) x. ( F ` C ) ) ) ) lim CC C ) )
158	101, 157	eleqtrrd 2257	. 2 |- ( ph -> ( ( K x. ( G ` C ) ) + ( L x. ( F ` C ) ) ) e. ( ( z e. { w e. X | w # C } |-> ( ( ( ( F oF x. G ) ` z ) - ( ( F oF x. G ) ` C ) ) / ( z - C ) ) ) lim CC C ) )
159		eqid 2177	. . 3 |- ( z e. { w e. X | w # C } |-> ( ( ( ( F oF x. G ) ` z ) - ( ( F oF x. G ) ` C ) ) / ( z - C ) ) ) = ( z e. { w e. X | w # C } |-> ( ( ( ( F oF x. G ) ` z ) - ( ( F oF x. G ) ` C ) ) / ( z - C ) ) )
160		mulcl 7938	. . . . 5 |- ( ( x e. CC /\ y e. CC ) -> ( x x. y ) e. CC )
161	160	adantl 277	. . . 4 |- ( ( ph /\ ( x e. CC /\ y e. CC ) ) -> ( x x. y ) e. CC )
162		inidm 3345	. . . 4 |- ( X i^i X ) = X
163	161, 6, 25, 135, 135, 162	off 6095	. . 3 |- ( ph -> ( F oF x. G ) : X --> CC )
164	2, 3, 159, 5, 163, 7	eldvap 14154	. 2 |- ( ph -> ( C ( S _D ( F oF x. G ) ) ( ( K x. ( G ` C ) ) + ( L x. ( F ` C ) ) ) <-> ( C e. ( ( int ` ( J ↾t S ) ) ` X ) /\ ( ( K x. ( G ` C ) ) + ( L x. ( F ` C ) ) ) e. ( ( z e. { w e. X | w # C } |-> ( ( ( ( F oF x. G ) ` z ) - ( ( F oF x. G ) ` C ) ) / ( z - C ) ) ) lim CC C ) ) ) )
165	10, 158, 164	mpbir2and 944	1 |- ( ph -> C ( S _D ( F oF x. G ) ) ( ( K x. ( G ` C ) ) + ( L x. ( F ` C ) ) ) )

Syntax hints:   -> wi 4   /\ wa 104   <-> wb 105   = wceq 1353   e. wcel 2148   {crab 2459   _Vcvv 2738   i^i cin 3129   C_ wss 3130   <.cop 3596   U.cuni 3810   class class class wbr 4004   |-> cmpt 4065   X. cxp 4625   dom cdm 4627   |` cres 4629   o. ccom 4631   Rel wrel 4632   Fn wfn 5212   -->wf 5213   ` cfv 5217  (class class class)co 5875   oFcof 6081   ^pm cpm 6649   CCcc 7809   + caddc 7814   x. cmul 7816   - cmin 8128   # cap 8538   / cdiv 8629   abscabs 11006   ↾_t crest 12688   MetOpencmopn 13448   Topctop 13500  TopOnctopon 13513   intcnt 13596   Cn ccn 13688   CnP ccnp 13689   tX ctx 13755   -cn->ccncf 14060   lim CC climc 14126   _D cdv 14127

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-ia1 106  ax-ia2 107  ax-ia3 108  ax-in1 614  ax-in2 615  ax-io 709  ax-5 1447  ax-7 1448  ax-gen 1449  ax-ie1 1493  ax-ie2 1494  ax-8 1504  ax-10 1505  ax-11 1506  ax-i12 1507  ax-bndl 1509  ax-4 1510  ax-17 1526  ax-i9 1530  ax-ial 1534  ax-i5r 1535  ax-13 2150  ax-14 2151  ax-ext 2159  ax-coll 4119  ax-sep 4122  ax-nul 4130  ax-pow 4175  ax-pr 4210  ax-un 4434  ax-setind 4537  ax-iinf 4588  ax-cnex 7902  ax-resscn 7903  ax-1cn 7904  ax-1re 7905  ax-icn 7906  ax-addcl 7907  ax-addrcl 7908  ax-mulcl 7909  ax-mulrcl 7910  ax-addcom 7911  ax-mulcom 7912  ax-addass 7913  ax-mulass 7914  ax-distr 7915  ax-i2m1 7916  ax-0lt1 7917  ax-1rid 7918  ax-0id 7919  ax-rnegex 7920  ax-precex 7921  ax-cnre 7922  ax-pre-ltirr 7923  ax-pre-ltwlin 7924  ax-pre-lttrn 7925  ax-pre-apti 7926  ax-pre-ltadd 7927  ax-pre-mulgt0 7928  ax-pre-mulext 7929  ax-arch 7930  ax-caucvg 7931  ax-addf 7933  ax-mulf 7934

This theorem depends on definitions:  df-bi 117  df-stab 831  df-dc 835  df-3or 979  df-3an 980  df-tru 1356  df-fal 1359  df-nf 1461  df-sb 1763  df-eu 2029  df-mo 2030  df-clab 2164  df-cleq 2170  df-clel 2173  df-nfc 2308  df-ne 2348  df-nel 2443  df-ral 2460  df-rex 2461  df-reu 2462  df-rmo 2463  df-rab 2464  df-v 2740  df-sbc 2964  df-csb 3059  df-dif 3132  df-un 3134  df-in 3136  df-ss 3143  df-nul 3424  df-if 3536  df-pw 3578  df-sn 3599  df-pr 3600  df-op 3602  df-uni 3811  df-int 3846  df-iun 3889  df-br 4005  df-opab 4066  df-mpt 4067  df-tr 4103  df-id 4294  df-po 4297  df-iso 4298  df-iord 4367  df-on 4369  df-ilim 4370  df-suc 4372  df-iom 4591  df-xp 4633  df-rel 4634  df-cnv 4635  df-co 4636  df-dm 4637  df-rn 4638  df-res 4639  df-ima 4640  df-iota 5179  df-fun 5219  df-fn 5220  df-f 5221  df-f1 5222  df-fo 5223  df-f1o 5224  df-fv 5225  df-isom 5226  df-riota 5831  df-ov 5878  df-oprab 5879  df-mpo 5880  df-of 6083  df-1st 6141  df-2nd 6142  df-recs 6306  df-frec 6392  df-map 6650  df-pm 6651  df-sup 6983  df-inf 6984  df-pnf 7994  df-mnf 7995  df-xr 7996  df-ltxr 7997  df-le 7998  df-sub 8130  df-neg 8131  df-reap 8532  df-ap 8539  df-div 8630  df-inn 8920  df-2 8978  df-3 8979  df-4 8980  df-n0 9177  df-z 9254  df-uz 9529  df-q 9620  df-rp 9654  df-xneg 9772  df-xadd 9773  df-seqfrec 10446  df-exp 10520  df-cj 10851  df-re 10852  df-im 10853  df-rsqrt 11007  df-abs 11008  df-rest 12690  df-topgen 12709  df-psmet 13450  df-xmet 13451  df-met 13452  df-bl 13453  df-mopn 13454  df-top 13501  df-topon 13514  df-bases 13546  df-ntr 13599  df-cn 13691  df-cnp 13692  df-tx 13756  df-cncf 14061  df-limced 14128  df-dvap 14129

This theorem is referenced by:  dvmulxx  14171  dvimulf  14173  dvef  14191