Description: Define a general-purpose
operation that builds a recursive sequence
(i.e., a function on an upper integer set such as 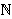 or or 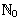 )
whose value at an index is a function of its previous value and the
value of an input sequence at that index. This definition is
complicated, but fortunately it is not intended to be used directly.
Instead, the only purpose of this definition is to provide us with an
object that has the properties expressed by seqf 10641, seq3-1 10639 and
seq3p1 10642. Typically, those are the main theorems
that would be used in
practice. )
whose value at an index is a function of its previous value and the
value of an input sequence at that index. This definition is
complicated, but fortunately it is not intended to be used directly.
Instead, the only purpose of this definition is to provide us with an
object that has the properties expressed by seqf 10641, seq3-1 10639 and
seq3p1 10642. Typically, those are the main theorems
that would be used in
practice.
The first operand in the parentheses is the operation that is applied to
the previous value and the value of the input sequence (second operand).
The operand to the left of the parenthesis is the integer to start from.
For example, for the operation 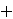 , an input sequence , an input sequence  with
values 1, 1/2, 1/4, 1/8,... would be transformed into the output
sequence with
values 1, 1/2, 1/4, 1/8,... would be transformed into the output
sequence 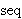 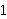  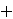    with values 1, 3/2, 7/4,
15/8,.., so that with values 1, 3/2, 7/4,
15/8,.., so that
 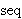 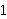  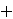     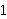   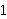 , ,
 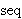 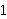  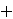     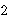   3/2,
etc. In other words, 3/2,
etc. In other words, 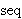 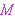  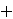    transforms a sequence transforms a sequence  into an infinite series.
into an infinite series. 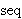 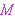  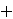    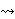 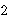 means "the sum of
F(n) from n = M to infinity is 2". Since limits are unique
(climuni 11689), by climdm 11691 the "sum of F(n) from n = 1 to
infinity" can
be expressed as means "the sum of
F(n) from n = M to infinity is 2". Since limits are unique
(climuni 11689), by climdm 11691 the "sum of F(n) from n = 1 to
infinity" can
be expressed as 
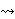
 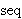 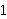  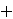     (provided
the sequence
converges) and evaluates to 2 in this example. (provided
the sequence
converges) and evaluates to 2 in this example.
Internally, the frec function generates as its values a set of
ordered pairs starting at 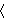 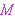     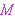  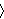 , with the first
member of each pair incremented by one in each successive value. So,
the range of frec is exactly the sequence we want, and we just
extract the range and throw away the domain. , with the first
member of each pair incremented by one in each successive value. So,
the range of frec is exactly the sequence we want, and we just
extract the range and throw away the domain.
(Contributed by NM, 18-Apr-2005.) (Revised by Jim Kingdon,
4-Nov-2022.) |