| Step | Hyp | Ref
| Expression |
|---|
| 1 | | ncfinraise 4482 |
. . . . . . . . 9
     Nn Nn      
       Nn Nn   1 1  
   1 1      |
| 2 | | anidm 625 |
. . . . . . . . . 10
    1 1 
    1 1 
     1 1 
   |
| 3 | 2 | rexbii 2640 |
. . . . . . . . 9
     Nn
Nn   1 1 
    1 1 
       Nn Nn  1 1 
   |
| 4 | 1, 3 | sylib 188 |
. . . . . . . 8
     Nn Nn      
       Nn Nn  1 1     |
| 5 | 4 | 3anidm23 1241 |
. . . . . . 7
     Nn Nn          Nn Nn  1 1     |
| 6 | 5 | ex 423 |
. . . . . 6
    Nn Nn          Nn Nn  1 1 
    |
| 7 | 6 | ancld 536 |
. . . . 5
    Nn Nn               Nn Nn  1 1 
     |
| 8 | 7 | eximdv 1622 |
. . . 4
    Nn Nn                   Nn Nn  1 1 
     |
| 9 | 8 | imp 418 |
. . 3
     Nn Nn                   Nn Nn  1 1      |
| 10 | | n0 3560 |
. . . 4
    

   
  |
| 11 | 10 | anbi2i 675 |
. . 3
     Nn Nn        
 Nn Nn         |
| 12 | | rexcom 2773 |
. . . 4
     Nn
Nn  
   1 1            Nn Nn  1 1     |
| 13 | | df-rex 2621 |
. . . 4
    
    Nn Nn  1 1        
      Nn Nn  1 1 
    |
| 14 | 12, 13 | bitri 240 |
. . 3
     Nn
Nn  
   1 1        
      Nn Nn  1 1 
    |
| 15 | 9, 11, 14 | 3imtr4i 257 |
. 2
     Nn Nn          Nn Nn      1 1     |
| 16 | | pw1eq 4144 |
. . . . . . . 8
       1 1    1 1   |
| 17 | 16 | eleq1d 2419 |
. . . . . . 7
        1 1      1 1      |
| 18 | 17 | cbvrexv 2837 |
. . . . . 6
    
  1 1          1 1 
   |
| 19 | 18 | anbi2i 675 |
. . . . 5
    
   1 1          1 1         
  1 1       
  1 1      |
| 20 | | reeanv 2779 |
. . . . 5
    
       1 1      1 1         
  1 1       
  1 1      |
| 21 | 19, 20 | bitr4i 243 |
. . . 4
    
   1 1          1 1                1 1      1 1      |
| 22 | | simplll 734 |
. . . . . . . 8
       Nn Nn          Nn
Nn  
 Nn Nn      
   
      1 1      1 1          Nn Nn  |
| 23 | | simprll 738 |
. . . . . . . 8
       Nn Nn          Nn
Nn  
 Nn Nn      
   
      1 1      1 1            |
| 24 | | simprlr 739 |
. . . . . . . 8
       Nn Nn          Nn
Nn  
 Nn Nn      
   
      1 1      1 1            |
| 25 | | ncfinraise 4482 |
. . . . . . . 8
     Nn Nn      
       Nn Nn   1 1  
   1 1      |
| 26 | 22, 23, 24, 25 | syl3anc 1182 |
. . . . . . 7
       Nn Nn          Nn
Nn  
 Nn Nn      
   
      1 1      1 1           Nn Nn   1 1 
    1 1 
    |
| 27 | | simp1rl 1020 |
. . . . . . . . . . . 12
       Nn Nn          Nn
Nn  
 Nn Nn      
   
      1 1      1 1        
 Nn Nn    1 1      1 1          Nn Nn  |
| 28 | | simp3l 983 |
. . . . . . . . . . . 12
       Nn Nn          Nn
Nn  
 Nn Nn      
   
      1 1      1 1        
 Nn Nn    1 1      1 1          Nn Nn  |
| 29 | | simp2rl 1024 |
. . . . . . . . . . . 12
       Nn Nn          Nn
Nn  
 Nn Nn      
   
      1 1      1 1        
 Nn Nn    1 1      1 1         1 1 
   |
| 30 | | simp3rl 1028 |
. . . . . . . . . . . 12
       Nn Nn          Nn
Nn  
 Nn Nn      
   
      1 1      1 1        
 Nn Nn    1 1      1 1         1 1 
   |
| 31 | | nnceleq 4431 |
. . . . . . . . . . . 12
      Nn Nn    Nn Nn     1 1  
   1 1           |
| 32 | 27, 28, 29, 30, 31 | syl22anc 1183 |
. . . . . . . . . . 11
       Nn Nn          Nn
Nn  
 Nn Nn      
   
      1 1      1 1        
 Nn Nn    1 1      1 1            |
| 33 | | simp1rr 1021 |
. . . . . . . . . . . 12
       Nn Nn          Nn
Nn  
 Nn Nn      
   
      1 1      1 1        
 Nn Nn    1 1      1 1          Nn Nn  |
| 34 | | simp2rr 1025 |
. . . . . . . . . . . 12
       Nn Nn          Nn
Nn  
 Nn Nn      
   
      1 1      1 1        
 Nn Nn    1 1      1 1         1 1 
   |
| 35 | | simp3rr 1029 |
. . . . . . . . . . . 12
       Nn Nn          Nn
Nn  
 Nn Nn      
   
      1 1      1 1        
 Nn Nn    1 1      1 1         1 1 
   |
| 36 | | nnceleq 4431 |
. . . . . . . . . . . 12
      Nn Nn    Nn Nn     1 1  
   1 1           |
| 37 | 33, 28, 34, 35, 36 | syl22anc 1183 |
. . . . . . . . . . 11
       Nn Nn          Nn
Nn  
 Nn Nn      
   
      1 1      1 1        
 Nn Nn    1 1      1 1            |
| 38 | 32, 37 | eqtr4d 2388 |
. . . . . . . . . 10
       Nn Nn          Nn
Nn  
 Nn Nn      
   
      1 1      1 1        
 Nn Nn    1 1      1 1            |
| 39 | 38 | 3expa 1151 |
. . . . . . . . 9
        Nn Nn          Nn Nn    Nn Nn      
   
      1 1      1 1           Nn Nn    1 1      1 1            |
| 40 | 39 | exp32 588 |
. . . . . . . 8
       Nn Nn          Nn
Nn  
 Nn Nn      
   
      1 1      1 1           Nn Nn     1 1  
   1 1            |
| 41 | 40 | rexlimdv 2738 |
. . . . . . 7
       Nn Nn          Nn
Nn  
 Nn Nn      
   
      1 1      1 1            Nn Nn   1 1  
   1 1           |
| 42 | 26, 41 | mpd 14 |
. . . . . 6
       Nn Nn          Nn
Nn  
 Nn Nn      
   
      1 1      1 1            |
| 43 | 42 | exp32 588 |
. . . . 5
      Nn Nn          Nn Nn    Nn Nn      
   
       1 1  
   1 1            |
| 44 | 43 | rexlimdvv 2745 |
. . . 4
      Nn Nn          Nn Nn    Nn Nn      
   
    1 1 
    1 1 
         |
| 45 | 21, 44 | syl5bi 208 |
. . 3
      Nn Nn          Nn Nn    Nn Nn           1 1          1 1       
   |
| 46 | 45 | ralrimivva 2707 |
. 2
     Nn Nn          Nn Nn    Nn Nn        1 1 
        1 1           |
| 47 | | eleq2 2414 |
. . . 4
        1 1      1 1      |
| 48 | 47 | rexbidv 2636 |
. . 3
        
   1 1          1 1 
    |
| 49 | 48 | reu4 3031 |
. 2
  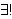   Nn Nn      1 1         Nn
Nn  
   1 1        Nn Nn    Nn Nn        1 1 
        1 1            |
| 50 | 15, 46, 49 | sylanbrc 645 |
1
     Nn Nn       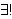   Nn Nn      1 1     |