| Step | Hyp | Ref
| Expression |
|---|
| 1 | | nulnnc 6119 |
. . . . . . 7
    NC NC |
| 2 | | eleq1 2413 |
. . . . . . 7
    
    NC
NC    NC NC   |
| 3 | 1, 2 | mtbiri 294 |
. . . . . 6
    
    NC NC  |
| 4 | 3 | necon2ai 2562 |
. . . . 5
    NC NC      |
| 5 | | n0 3560 |
. . . . 5
    

   
  |
| 6 | 4, 5 | sylib 188 |
. . . 4
    NC NC        |
| 7 | | vex 2863 |
. . . . . . . . . 10
    |
| 8 | 7 | pw1ex 4304 |
. . . . . . . . 9
  1 1    |
| 9 | 8 | ncelncsi 6122 |
. . . . . . . 8
 Nc Nc  1 1 
 NC NC |
| 10 | | eqid 2353 |
. . . . . . . 8
 Nc Nc  1 1 
 Nc Nc  1 1  |
| 11 | | eqeq1 2359 |
. . . . . . . . 9
    Nc Nc  1 1      Nc Nc  1 1   Nc Nc  1 1 
 Nc Nc  1 1    |
| 12 | 11 | rspcev 2956 |
. . . . . . . 8
   Nc Nc  1 1   NC NC  Nc Nc  1 1 
 Nc Nc  1 1       NC
NC   Nc Nc  1 1   |
| 13 | 9, 10, 12 | mp2an 653 |
. . . . . . 7
    NC NC   Nc Nc  1 1  |
| 14 | 13 | jctr 526 |
. . . . . 6
        
     NC NC   Nc Nc  1 1    |
| 15 | 14 | a1i 10 |
. . . . 5
    NC NC               NC NC   Nc Nc  1 1     |
| 16 | 15 | eximdv 1622 |
. . . 4
    NC NC                   NC NC   Nc Nc  1 1     |
| 17 | 6, 16 | mpd 14 |
. . 3
    NC NC            NC
NC   Nc Nc  1 1    |
| 18 | | rexcom 2773 |
. . . 4
     NC
NC  
    Nc
Nc  1 1          NC NC   Nc Nc  1 1   |
| 19 | | df-rex 2621 |
. . . 4
    
    NC NC   Nc Nc  1 1             NC
NC   Nc Nc  1 1    |
| 20 | 18, 19 | bitri 240 |
. . 3
     NC
NC  
    Nc
Nc  1 1             NC NC   Nc Nc  1 1    |
| 21 | 17, 20 | sylibr 203 |
. 2
    NC NC     NC NC       Nc
Nc  1 1   |
| 22 | | reeanv 2779 |
. . . 4
    
        Nc Nc  1 1     Nc
Nc  1 1  

   
   Nc Nc  1 1         Nc
Nc  1 1    |
| 23 | | ncseqnc 6129 |
. . . . . . . . . . . 12
    NC NC     Nc Nc        |
| 24 | 23 | biimpar 471 |
. . . . . . . . . . 11
     NC NC         Nc Nc   |
| 25 | 24 | adantrr 697 |
. . . . . . . . . 10
     NC NC               Nc
Nc   |
| 26 | | ncseqnc 6129 |
. . . . . . . . . . . 12
    NC NC     Nc Nc        |
| 27 | 26 | biimpar 471 |
. . . . . . . . . . 11
     NC NC         Nc Nc   |
| 28 | 27 | adantrl 696 |
. . . . . . . . . 10
     NC NC               Nc
Nc   |
| 29 | 25, 28 | eqtr3d 2387 |
. . . . . . . . 9
     NC NC             Nc Nc   Nc Nc   |
| 30 | 7 | ncpw1 6153 |
. . . . . . . . 9
  Nc Nc   Nc Nc   Nc Nc  1 1   Nc
Nc  1 1   |
| 31 | 29, 30 | sylib 188 |
. . . . . . . 8
     NC NC             Nc Nc  1 1   Nc Nc  1 1   |
| 32 | 31 | 3adant2 974 |
. . . . . . 7
     NC NC     NC NC    NC NC        
   
 Nc Nc  1 1 
 Nc Nc  1 1   |
| 33 | | eqeq2 2362 |
. . . . . . . . 9
  Nc Nc  1 1 
 Nc Nc  1 1      Nc Nc  1 1     Nc Nc  1 1    |
| 34 | 33 | anbi1d 685 |
. . . . . . . 8
  Nc Nc  1 1 
 Nc Nc  1 1       Nc Nc  1 1 
   Nc Nc  1 1       Nc Nc  1 1     Nc
Nc  1 1     |
| 35 | | eqtr3 2372 |
. . . . . . . 8
     Nc Nc  1 1     Nc Nc  1 1        |
| 36 | 34, 35 | syl6bi 219 |
. . . . . . 7
  Nc Nc  1 1 
 Nc Nc  1 1       Nc Nc  1 1 
   Nc Nc  1 1         |
| 37 | 32, 36 | syl 15 |
. . . . . 6
     NC NC     NC NC    NC NC        
   
   
 Nc Nc  1 1 
   Nc Nc  1 1         |
| 38 | 37 | 3expa 1151 |
. . . . 5
      NC NC     NC NC    NC NC                   Nc Nc  1 1 
   Nc Nc  1 1         |
| 39 | 38 | rexlimdvva 2746 |
. . . 4
     NC NC     NC NC    NC NC       
        Nc Nc  1 1     Nc
Nc  1 1  
      |
| 40 | 22, 39 | syl5bir 209 |
. . 3
     NC NC     NC NC    NC NC       
    Nc
Nc  1 1         Nc Nc  1 1         |
| 41 | 40 | ralrimivva 2707 |
. 2
    NC NC     NC NC    NC NC         Nc Nc  1 1 
       Nc Nc  1 1         |
| 42 | | eqeq1 2359 |
. . . . 5
         Nc
Nc  1 1     Nc Nc  1 1    |
| 43 | 42 | rexbidv 2636 |
. . . 4
        
    Nc
Nc  1 1         Nc Nc  1 1    |
| 44 | | pw1eq 4144 |
. . . . . . 7
       1 1    1 1   |
| 45 | 44 | nceqd 6111 |
. . . . . 6
      Nc Nc  1 1 
 Nc Nc  1 1   |
| 46 | 45 | eqeq2d 2364 |
. . . . 5
         Nc
Nc  1 1     Nc Nc  1 1    |
| 47 | 46 | cbvrexv 2837 |
. . . 4
    
   Nc Nc  1 1         Nc
Nc  1 1   |
| 48 | 43, 47 | syl6bb 252 |
. . 3
        
    Nc
Nc  1 1         Nc Nc  1 1    |
| 49 | 48 | reu4 3031 |
. 2
  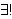   NC NC       Nc
Nc  1 1       NC NC   
   Nc Nc  1 1      NC NC    NC NC         Nc Nc  1 1 
       Nc Nc  1 1          |
| 50 | 21, 41, 49 | sylanbrc 645 |
1
    NC NC  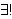   NC NC       Nc
Nc  1 1   |