Theorem axrep 220

Description: Axiom of Replacement. An axiom scheme of Zermelo-Fraenkel set theory. Axiom 5 of [TakeutiZaring] p. 19. (Contributed by Mario Carneiro, 10-Oct-2014.)

Hypotheses

Ref	Expression
axrep.1	|- A:*
axrep.2	|- B:(al -> *)

Assertion

Ref	Expression
axrep	|- T. |= [(A.\x:al (E.\y:be (A.\z:be [(A.\y:be A) ==> [z:be = y:be]]))) ==> (E.\y:(be -> *) (A.\z:be [(y:(be -> *)z:be) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])]))]

Distinct variable groups:   y,B   al,y   x,y,be   y,z,be

Proof of Theorem axrep

Dummy variable f is distinct from all other variables.

Step	Hyp	Ref	Expression
1		wal 134	. . . . . . 7 |- A.:((al -> *) -> *)
2		wex 139	. . . . . . . . 9 |- E.:((be -> *) -> *)
3		wal 134	. . . . . . . . . . 11 |- A.:((be -> *) -> *)
4		wim 137	. . . . . . . . . . . . 13 |- ==> :(* -> (* -> *))
5		axrep.1	. . . . . . . . . . . . . . 15 |- A:*
6	5	wl 66	. . . . . . . . . . . . . 14 |- \y:be A:(be -> *)
7	3, 6	wc 50	. . . . . . . . . . . . 13 |- (A.\y:be A):*
8		wv 64	. . . . . . . . . . . . . 14 |- z:be:be
9		wv 64	. . . . . . . . . . . . . 14 |- y:be:be
10	8, 9	weqi 76	. . . . . . . . . . . . 13 |- [z:be = y:be]:*
11	4, 7, 10	wov 72	. . . . . . . . . . . 12 |- [(A.\y:be A) ==> [z:be = y:be]]:*
12	11	wl 66	. . . . . . . . . . 11 |- \z:be [(A.\y:be A) ==> [z:be = y:be]]:(be -> *)
13	3, 12	wc 50	. . . . . . . . . 10 |- (A.\z:be [(A.\y:be A) ==> [z:be = y:be]]):*
14	13	wl 66	. . . . . . . . 9 |- \y:be (A.\z:be [(A.\y:be A) ==> [z:be = y:be]]):(be -> *)
15	2, 14	wc 50	. . . . . . . 8 |- (E.\y:be (A.\z:be [(A.\y:be A) ==> [z:be = y:be]])):*
16	15	wl 66	. . . . . . 7 |- \x:al (E.\y:be (A.\z:be [(A.\y:be A) ==> [z:be = y:be]])):(al -> *)
17	1, 16	wc 50	. . . . . 6 |- (A.\x:al (E.\y:be (A.\z:be [(A.\y:be A) ==> [z:be = y:be]]))):*
18		wtru 43	. . . . . . . 8 |- T.:*
19		wex 139	. . . . . . . . 9 |- E.:((al -> *) -> *)
20		wan 136	. . . . . . . . . . 11 |- /\ :(* -> (* -> *))
21		axrep.2	. . . . . . . . . . . 12 |- B:(al -> *)
22		wv 64	. . . . . . . . . . . 12 |- x:al:al
23	21, 22	wc 50	. . . . . . . . . . 11 |- (Bx:al):*
24	20, 23, 7	wov 72	. . . . . . . . . 10 |- [(Bx:al) /\ (A.\y:be A)]:*
25	24	wl 66	. . . . . . . . 9 |- \x:al [(Bx:al) /\ (A.\y:be A)]:(al -> *)
26	19, 25	wc 50	. . . . . . . 8 |- (E.\x:al [(Bx:al) /\ (A.\y:be A)]):*
27	18, 26	eqid 83	. . . . . . 7 |- T. |= [(E.\x:al [(Bx:al) /\ (A.\y:be A)]) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])]
28	27	alrimiv 151	. . . . . 6 |- T. |= (A.\z:be [(E.\x:al [(Bx:al) /\ (A.\y:be A)]) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])])
29	17, 28	a1i 28	. . . . 5 |- (A.\x:al (E.\y:be (A.\z:be [(A.\y:be A) ==> [z:be = y:be]]))) |= (A.\z:be [(E.\x:al [(Bx:al) /\ (A.\y:be A)]) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])])
30	29	ax-cb1 29	. . . . . 6 |- (A.\x:al (E.\y:be (A.\z:be [(A.\y:be A) ==> [z:be = y:be]]))):*
31		wv 64	. . . . . . . . . . 11 |- y:(be -> *):(be -> *)
32	31, 8	wc 50	. . . . . . . . . 10 |- (y:(be -> *)z:be):*
33	32, 26	weqi 76	. . . . . . . . 9 |- [(y:(be -> *)z:be) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])]:*
34	33	wl 66	. . . . . . . 8 |- \z:be [(y:(be -> *)z:be) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])]:(be -> *)
35	3, 34	wc 50	. . . . . . 7 |- (A.\z:be [(y:(be -> *)z:be) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])]):*
36	26	wl 66	. . . . . . 7 |- \z:be (E.\x:al [(Bx:al) /\ (A.\y:be A)]):(be -> *)
37		weq 41	. . . . . . . . . 10 |- = :(* -> (* -> *))
38	31, 36	weqi 76	. . . . . . . . . . . . 13 |- [y:(be -> *) = \z:be (E.\x:al [(Bx:al) /\ (A.\y:be A)])]:*
39	38	id 25	. . . . . . . . . . . 12 |- [y:(be -> *) = \z:be (E.\x:al [(Bx:al) /\ (A.\y:be A)])] |= [y:(be -> *) = \z:be (E.\x:al [(Bx:al) /\ (A.\y:be A)])]
40	31, 8, 39	ceq1 89	. . . . . . . . . . 11 |- [y:(be -> *) = \z:be (E.\x:al [(Bx:al) /\ (A.\y:be A)])] |= [(y:(be -> *)z:be) = (\z:be (E.\x:al [(Bx:al) /\ (A.\y:be A)])z:be)]
41	26	beta 92	. . . . . . . . . . . 12 |- T. |= [(\z:be (E.\x:al [(Bx:al) /\ (A.\y:be A)])z:be) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])]
42	38, 41	a1i 28	. . . . . . . . . . 11 |- [y:(be -> *) = \z:be (E.\x:al [(Bx:al) /\ (A.\y:be A)])] |= [(\z:be (E.\x:al [(Bx:al) /\ (A.\y:be A)])z:be) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])]
43	32, 40, 42	eqtri 95	. . . . . . . . . 10 |- [y:(be -> *) = \z:be (E.\x:al [(Bx:al) /\ (A.\y:be A)])] |= [(y:(be -> *)z:be) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])]
44	37, 32, 26, 43	oveq1 99	. . . . . . . . 9 |- [y:(be -> *) = \z:be (E.\x:al [(Bx:al) /\ (A.\y:be A)])] |= [[(y:(be -> *)z:be) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])] = [(E.\x:al [(Bx:al) /\ (A.\y:be A)]) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])]]
45		weq 41	. . . . . . . . . 10 |- = :((be -> *) -> ((be -> *) -> *))
46		wv 64	. . . . . . . . . 10 |- f:be:be
47	37, 46	ax-17 105	. . . . . . . . . 10 |- T. |= [(\z:be = f:be) = = ]
48	31, 46	ax-17 105	. . . . . . . . . 10 |- T. |= [(\z:be y:(be -> *)f:be) = y:(be -> *)]
49	26, 46	ax-hbl1 103	. . . . . . . . . 10 |- T. |= [(\z:be \z:be (E.\x:al [(Bx:al) /\ (A.\y:be A)])f:be) = \z:be (E.\x:al [(Bx:al) /\ (A.\y:be A)])]
50	45, 31, 46, 36, 47, 48, 49	hbov 111	. . . . . . . . 9 |- T. |= [(\z:be [y:(be -> *) = \z:be (E.\x:al [(Bx:al) /\ (A.\y:be A)])]f:be) = [y:(be -> *) = \z:be (E.\x:al [(Bx:al) /\ (A.\y:be A)])]]
51	33, 44, 50	leqf 181	. . . . . . . 8 |- [y:(be -> *) = \z:be (E.\x:al [(Bx:al) /\ (A.\y:be A)])] |= [\z:be [(y:(be -> *)z:be) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])] = \z:be [(E.\x:al [(Bx:al) /\ (A.\y:be A)]) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])]]
52	3, 34, 51	ceq2 90	. . . . . . 7 |- [y:(be -> *) = \z:be (E.\x:al [(Bx:al) /\ (A.\y:be A)])] |= [(A.\z:be [(y:(be -> *)z:be) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])]) = (A.\z:be [(E.\x:al [(Bx:al) /\ (A.\y:be A)]) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])])]
53	26, 26	weqi 76	. . . . . . . . 9 |- [(E.\x:al [(Bx:al) /\ (A.\y:be A)]) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])]:*
54	53	wl 66	. . . . . . . 8 |- \z:be [(E.\x:al [(Bx:al) /\ (A.\y:be A)]) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])]:(be -> *)
55		wv 64	. . . . . . . 8 |- f:(be -> *):(be -> *)
56	3, 55	ax-17 105	. . . . . . . 8 |- T. |= [(\y:(be -> *) A.f:(be -> *)) = A.]
57		weq 41	. . . . . . . . . . 11 |- = :(ga -> (ga -> *))
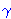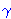
58	57, 55	ax-17 105	. . . . . . . . . 10 |- T. |= [(\y:(be -> *) = f:(be -> *)) = = ]
59	2, 55	ax-17 105	. . . . . . . . . . 11 |- T. |= [(\y:(be -> *) E.f:(be -> *)) = E.]
60	20, 55	ax-17 105	. . . . . . . . . . . . 13 |- T. |= [(\y:(be -> *) /\ f:(be -> *)) = /\ ]
61	23, 55	ax-17 105	. . . . . . . . . . . . 13 |- T. |= [(\y:(be -> *) (Bx:al)f:(be -> *)) = (Bx:al)]
62	5, 55, 18	hbl1 104	. . . . . . . . . . . . . 14 |- T. |= [(\y:(be -> *) \y:be Af:(be -> *)) = \y:be A]
63	3, 6, 55, 56, 62	hbc 110	. . . . . . . . . . . . 13 |- T. |= [(\y:(be -> *) (A.\y:be A)f:(be -> *)) = (A.\y:be A)]
64	20, 23, 55, 7, 60, 61, 63	hbov 111	. . . . . . . . . . . 12 |- T. |= [(\y:(be -> *) [(Bx:al) /\ (A.\y:be A)]f:(be -> *)) = [(Bx:al) /\ (A.\y:be A)]]
65	24, 55, 64	hbl 112	. . . . . . . . . . 11 |- T. |= [(\y:(be -> *) \x:al [(Bx:al) /\ (A.\y:be A)]f:(be -> *)) = \x:al [(Bx:al) /\ (A.\y:be A)]]
66	19, 25, 55, 59, 65	hbc 110	. . . . . . . . . 10 |- T. |= [(\y:(be -> *) (E.\x:al [(Bx:al) /\ (A.\y:be A)])f:(be -> *)) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])]
67	37, 26, 55, 26, 58, 66, 66	hbov 111	. . . . . . . . 9 |- T. |= [(\y:(be -> *) [(E.\x:al [(Bx:al) /\ (A.\y:be A)]) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])]f:(be -> *)) = [(E.\x:al [(Bx:al) /\ (A.\y:be A)]) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])]]
68	53, 55, 67	hbl 112	. . . . . . . 8 |- T. |= [(\y:(be -> *) \z:be [(E.\x:al [(Bx:al) /\ (A.\y:be A)]) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])]f:(be -> *)) = \z:be [(E.\x:al [(Bx:al) /\ (A.\y:be A)]) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])]]
69	3, 54, 55, 56, 68	hbc 110	. . . . . . 7 |- T. |= [(\y:(be -> *) (A.\z:be [(E.\x:al [(Bx:al) /\ (A.\y:be A)]) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])])f:(be -> *)) = (A.\z:be [(E.\x:al [(Bx:al) /\ (A.\y:be A)]) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])])]
70	26, 55, 66	hbl 112	. . . . . . 7 |- T. |= [(\y:(be -> *) \z:be (E.\x:al [(Bx:al) /\ (A.\y:be A)])f:(be -> *)) = \z:be (E.\x:al [(Bx:al) /\ (A.\y:be A)])]
71	35, 36, 52, 69, 70	clf 115	. . . . . 6 |- T. |= [(\y:(be -> *) (A.\z:be [(y:(be -> *)z:be) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])])\z:be (E.\x:al [(Bx:al) /\ (A.\y:be A)])) = (A.\z:be [(E.\x:al [(Bx:al) /\ (A.\y:be A)]) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])])]
72	30, 71	a1i 28	. . . . 5 |- (A.\x:al (E.\y:be (A.\z:be [(A.\y:be A) ==> [z:be = y:be]]))) |= [(\y:(be -> *) (A.\z:be [(y:(be -> *)z:be) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])])\z:be (E.\x:al [(Bx:al) /\ (A.\y:be A)])) = (A.\z:be [(E.\x:al [(Bx:al) /\ (A.\y:be A)]) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])])]
73	29, 72	mpbir 87	. . . 4 |- (A.\x:al (E.\y:be (A.\z:be [(A.\y:be A) ==> [z:be = y:be]]))) |= (\y:(be -> *) (A.\z:be [(y:(be -> *)z:be) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])])\z:be (E.\x:al [(Bx:al) /\ (A.\y:be A)]))
74	35	wl 66	. . . . 5 |- \y:(be -> *) (A.\z:be [(y:(be -> *)z:be) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])]):((be -> *) -> *)
75	74, 36	ax4e 168	. . . 4 |- (\y:(be -> *) (A.\z:be [(y:(be -> *)z:be) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])])\z:be (E.\x:al [(Bx:al) /\ (A.\y:be A)])) |= (E.\y:(be -> *) (A.\z:be [(y:(be -> *)z:be) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])]))
76	73, 75	syl 16	. . 3 |- (A.\x:al (E.\y:be (A.\z:be [(A.\y:be A) ==> [z:be = y:be]]))) |= (E.\y:(be -> *) (A.\z:be [(y:(be -> *)z:be) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])]))
77	76, 18	adantl 56	. 2 |- (T., (A.\x:al (E.\y:be (A.\z:be [(A.\y:be A) ==> [z:be = y:be]])))) |= (E.\y:(be -> *) (A.\z:be [(y:(be -> *)z:be) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])]))
78	77	ex 158	1 |- T. |= [(A.\x:al (E.\y:be (A.\z:be [(A.\y:be A) ==> [z:be = y:be]]))) ==> (E.\y:(be -> *) (A.\z:be [(y:(be -> *)z:be) = (E.\x:al [(Bx:al) /\ (A.\y:be A)])]))]

Syntax hints:  tv 1   -> ht 2  *hb 3  kc 5  \kl 6   = ke 7  T.kt 8  [kbr 9   |= wffMMJ2 11  wffMMJ2t 12   /\ tan 119   ==> tim 121  A.tal 122  E.tex 123

This theorem was proved from axioms:  ax-syl 15  ax-jca 17  ax-simpl 20  ax-simpr 21  ax-id 24  ax-trud 26  ax-cb1 29  ax-cb2 30  ax-wctl 31  ax-wctr 32  ax-weq 40  ax-refl 42  ax-eqmp 45  ax-ded 46  ax-wct 47  ax-wc 49  ax-ceq 51  ax-wv 63  ax-wl 65  ax-beta 67  ax-distrc 68  ax-leq 69  ax-distrl 70  ax-wov 71  ax-eqtypi 77  ax-eqtypri 80  ax-hbl1 103  ax-17 105  ax-inst 113  ax-eta 177

This theorem depends on definitions:  df-ov 73  df-al 126  df-an 128  df-im 129  df-ex 131

This theorem is referenced by: (None)