Theorem enpw1 6063

Description: Two classes are equinumerous iff their unit power classes are equinumerous. Theorem XI.1.33 of [Rosser] p. 368. (Contributed by SF, 26-Feb-2015.)

Assertion

Ref	Expression
enpw1	|- (A ~~ B <-> ~P1 A ~~ ~P1 B)

Proof of Theorem enpw1

Dummy variables a b f g w x y z are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		brex 4690	. 2 |- (A ~~ B -> (A e. _V /\ B e. _V))
2		brex 4690	. . 3 |- (~P1 A ~~ ~P1 B -> (~P1 A e. _V /\ ~P1 B e. _V))
3		pw1exb 4327	. . . 4 |- (~P1 A e. _V <-> A e. _V)
4		pw1exb 4327	. . . 4 |- (~P1 B e. _V <-> B e. _V)
5	3, 4	anbi12i 678	. . 3 |- ((~P1 A e. _V /\ ~P1 B e. _V) <-> (A e. _V /\ B e. _V))
6	2, 5	sylib 188	. 2 |- (~P1 A ~~ ~P1 B -> (A e. _V /\ B e. _V))
7		breq1 4643	. . . 4 |- (a = A -> (a ~~ b <-> A ~~ b))
8		pw1eq 4144	. . . . 5 |- (a = A -> ~P1 a = ~P1 A)
9	8	breq1d 4650	. . . 4 |- (a = A -> (~P1 a ~~ ~P1 b <-> ~P1 A ~~ ~P1 b))
10	7, 9	bibi12d 312	. . 3 |- (a = A -> ((a ~~ b <-> ~P1 a ~~ ~P1 b) <-> (A ~~ b <-> ~P1 A ~~ ~P1 b)))
11		breq2 4644	. . . 4 |- (b = B -> (A ~~ b <-> A ~~ B))
12		pw1eq 4144	. . . . 5 |- (b = B -> ~P1 b = ~P1 B)
13	12	breq2d 4652	. . . 4 |- (b = B -> (~P1 A ~~ ~P1 b <-> ~P1 A ~~ ~P1 B))
14	11, 13	bibi12d 312	. . 3 |- (b = B -> ((A ~~ b <-> ~P1 A ~~ ~P1 b) <-> (A ~~ B <-> ~P1 A ~~ ~P1 B)))
15		bren 6031	. . . . 5 |- (a ~~ b <-> E.f f:a-1-1-onto->b)
16		f1ofun 5290	. . . . . . . . . 10 |- (f:a-1-1-onto->b -> Fun f)
17		funsi 5521	. . . . . . . . . 10 |- (Fun f -> Fun SI f)
18	16, 17	syl 15	. . . . . . . . 9 |- (f:a-1-1-onto->b -> Fun SI f)
19		f1odm 5291	. . . . . . . . . 10 |- (f:a-1-1-onto->b -> dom f = a)
20		dmsi 5520	. . . . . . . . . . 11 |- dom SI f = ~P1 dom f
21		pw1eq 4144	. . . . . . . . . . 11 |- (dom f = a -> ~P1 dom f = ~P1 a)
22	20, 21	syl5eq 2397	. . . . . . . . . 10 |- (dom f = a -> dom SI f = ~P1 a)
23	19, 22	syl 15	. . . . . . . . 9 |- (f:a-1-1-onto->b -> dom SI f = ~P1 a)
24		df-fn 4791	. . . . . . . . 9 |- ( SI f Fn ~P1 a <-> (Fun SI f /\ dom SI f = ~P1 a))
25	18, 23, 24	sylanbrc 645	. . . . . . . 8 |- (f:a-1-1-onto->b -> SI f Fn ~P1 a)
26		f1of1 5287	. . . . . . . . . . 11 |- (f:a-1-1-onto->b -> f:a-1-1->b)
27		df-f1 4793	. . . . . . . . . . . 12 |- (f:a-1-1->b <-> (f:a-->b /\ Fun `'f))
28	27	simprbi 450	. . . . . . . . . . 11 |- (f:a-1-1->b -> Fun `'f)
29		funsi 5521	. . . . . . . . . . 11 |- (Fun `'f -> Fun SI `'f)
30	26, 28, 29	3syl 18	. . . . . . . . . 10 |- (f:a-1-1-onto->b -> Fun SI `'f)
31		cnvsi 5519	. . . . . . . . . . 11 |- `' SI f = SI `'f
32	31	funeqi 5129	. . . . . . . . . 10 |- (Fun `' SI f <-> Fun SI `'f)
33	30, 32	sylibr 203	. . . . . . . . 9 |- (f:a-1-1-onto->b -> Fun `' SI f)
34		f1ofo 5294	. . . . . . . . . 10 |- (f:a-1-1-onto->b -> f:a-onto->b)
35		forn 5273	. . . . . . . . . 10 |- (f:a-onto->b -> ran f = b)
36		rnsi 5522	. . . . . . . . . . . 12 |- ran SI f = ~P1 ran f
37		dfrn4 4905	. . . . . . . . . . . 12 |- ran SI f = dom `' SI f
38	36, 37	eqtr3i 2375	. . . . . . . . . . 11 |- ~P1 ran f = dom `' SI f
39		pw1eq 4144	. . . . . . . . . . 11 |- (ran f = b -> ~P1 ran f = ~P1 b)
40	38, 39	syl5eqr 2399	. . . . . . . . . 10 |- (ran f = b -> dom `' SI f = ~P1 b)
41	34, 35, 40	3syl 18	. . . . . . . . 9 |- (f:a-1-1-onto->b -> dom `' SI f = ~P1 b)
42		df-fn 4791	. . . . . . . . 9 |- (`' SI f Fn ~P1 b <-> (Fun `' SI f /\ dom `' SI f = ~P1 b))
43	33, 41, 42	sylanbrc 645	. . . . . . . 8 |- (f:a-1-1-onto->b -> `' SI f Fn ~P1 b)
44		dff1o4 5295	. . . . . . . 8 |- ( SI f:~P1 a-1-1-onto->~P1 b <-> ( SI f Fn ~P1 a /\ `' SI f Fn ~P1 b))
45	25, 43, 44	sylanbrc 645	. . . . . . 7 |- (f:a-1-1-onto->b -> SI f:~P1 a-1-1-onto->~P1 b)
46		vex 2863	. . . . . . . . 9 |- f e. _V
47	46	siex 4754	. . . . . . . 8 |- SI f e. _V
48	47	f1oen 6034	. . . . . . 7 |- ( SI f:~P1 a-1-1-onto->~P1 b -> ~P1 a ~~ ~P1 b)
49	45, 48	syl 15	. . . . . 6 |- (f:a-1-1-onto->b -> ~P1 a ~~ ~P1 b)
50	49	exlimiv 1634	. . . . 5 |- (E.f f:a-1-1-onto->b -> ~P1 a ~~ ~P1 b)
51	15, 50	sylbi 187	. . . 4 |- (a ~~ b -> ~P1 a ~~ ~P1 b)
52		bren 6031	. . . . 5 |- (~P1 a ~~ ~P1 b <-> E.g g:~P1 a-1-1-onto->~P1 b)
53		f1ofun 5290	. . . . . . . . . . . . . 14 |- (g:~P1 a-1-1-onto->~P1 b -> Fun g)
54		fununiq 5518	. . . . . . . . . . . . . . . 16 |- ((Fun g /\ {x}g{y} /\ {x}g{z}) -> {y} = {z})
55		vex 2863	. . . . . . . . . . . . . . . . 17 |- y e. _V
56	55	sneqb 3877	. . . . . . . . . . . . . . . 16 |- ({y} = {z} <-> y = z)
57	54, 56	sylib 188	. . . . . . . . . . . . . . 15 |- ((Fun g /\ {x}g{y} /\ {x}g{z}) -> y = z)
58	57	3expib 1154	. . . . . . . . . . . . . 14 |- (Fun g -> (({x}g{y} /\ {x}g{z}) -> y = z))
59	53, 58	syl 15	. . . . . . . . . . . . 13 |- (g:~P1 a-1-1-onto->~P1 b -> (({x}g{y} /\ {x}g{z}) -> y = z))
60	59	alrimivv 1632	. . . . . . . . . . . 12 |- (g:~P1 a-1-1-onto->~P1 b -> A.yA.z(({x}g{y} /\ {x}g{z}) -> y = z))
61		sneq 3745	. . . . . . . . . . . . . 14 |- (y = z -> {y} = {z})
62	61	breq2d 4652	. . . . . . . . . . . . 13 |- (y = z -> ({x}g{y} <-> {x}g{z}))
63	62	mo4 2237	. . . . . . . . . . . 12 |- (E*y{x}g{y} <-> A.yA.z(({x}g{y} /\ {x}g{z}) -> y = z))
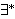64	60, 63	sylibr 203	. . . . . . . . . . 11 |- (g:~P1 a-1-1-onto->~P1 b -> E*y{x}g{y})
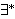65	64	alrimiv 1631	. . . . . . . . . 10 |- (g:~P1 a-1-1-onto->~P1 b -> A.xE*y{x}g{y})
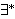66		funopab 5140	. . . . . . . . . 10 |- (Fun {<.x, y>. | {x}g{y}} <-> A.xE*y{x}g{y})
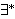67	65, 66	sylibr 203	. . . . . . . . 9 |- (g:~P1 a-1-1-onto->~P1 b -> Fun {<.x, y>. | {x}g{y}})
68		dmopab 4916	. . . . . . . . . 10 |- dom {<.x, y>. | {x}g{y}} = {x | E.y{x}g{y}}
69		eldm 4899	. . . . . . . . . . . . . . 15 |- ({x} e. dom g <-> E.z{x}gz)
70		brelrn 4961	. . . . . . . . . . . . . . . . 17 |- ({x}gz -> z e. ran g)
71		f1ofo 5294	. . . . . . . . . . . . . . . . . . . . 21 |- (g:~P1 a-1-1-onto->~P1 b -> g:~P1 a-onto->~P1 b)
72		forn 5273	. . . . . . . . . . . . . . . . . . . . 21 |- (g:~P1 a-onto->~P1 b -> ran g = ~P1 b)
73	71, 72	syl 15	. . . . . . . . . . . . . . . . . . . 20 |- (g:~P1 a-1-1-onto->~P1 b -> ran g = ~P1 b)
74	73	eleq2d 2420	. . . . . . . . . . . . . . . . . . 19 |- (g:~P1 a-1-1-onto->~P1 b -> (z e. ran g <-> z e. ~P1 b))
75		elpw1 4145	. . . . . . . . . . . . . . . . . . . 20 |- (z e. ~P1 b <-> E.w e. b z = {w})
76		breq2 4644	. . . . . . . . . . . . . . . . . . . . . 22 |- (z = {w} -> ({x}gz <-> {x}g{w}))
77		vex 2863	. . . . . . . . . . . . . . . . . . . . . . 23 |- w e. _V
78		sneq 3745	. . . . . . . . . . . . . . . . . . . . . . . 24 |- (y = w -> {y} = {w})
79	78	breq2d 4652	. . . . . . . . . . . . . . . . . . . . . . 23 |- (y = w -> ({x}g{y} <-> {x}g{w}))
80	77, 79	spcev 2947	. . . . . . . . . . . . . . . . . . . . . 22 |- ({x}g{w} -> E.y{x}g{y})
81	76, 80	syl6bi 219	. . . . . . . . . . . . . . . . . . . . 21 |- (z = {w} -> ({x}gz -> E.y{x}g{y}))
82	81	rexlimivw 2735	. . . . . . . . . . . . . . . . . . . 20 |- (E.w e. b z = {w} -> ({x}gz -> E.y{x}g{y}))
83	75, 82	sylbi 187	. . . . . . . . . . . . . . . . . . 19 |- (z e. ~P1 b -> ({x}gz -> E.y{x}g{y}))
84	74, 83	syl6bi 219	. . . . . . . . . . . . . . . . . 18 |- (g:~P1 a-1-1-onto->~P1 b -> (z e. ran g -> ({x}gz -> E.y{x}g{y})))
85	84	com23 72	. . . . . . . . . . . . . . . . 17 |- (g:~P1 a-1-1-onto->~P1 b -> ({x}gz -> (z e. ran g -> E.y{x}g{y})))
86	70, 85	mpdi 38	. . . . . . . . . . . . . . . 16 |- (g:~P1 a-1-1-onto->~P1 b -> ({x}gz -> E.y{x}g{y}))
87	86	exlimdv 1636	. . . . . . . . . . . . . . 15 |- (g:~P1 a-1-1-onto->~P1 b -> (E.z{x}gz -> E.y{x}g{y}))
88	69, 87	syl5bi 208	. . . . . . . . . . . . . 14 |- (g:~P1 a-1-1-onto->~P1 b -> ({x} e. dom g -> E.y{x}g{y}))
89		breldm 4912	. . . . . . . . . . . . . . 15 |- ({x}g{y} -> {x} e. dom g)
90	89	exlimiv 1634	. . . . . . . . . . . . . 14 |- (E.y{x}g{y} -> {x} e. dom g)
91	88, 90	impbid1 194	. . . . . . . . . . . . 13 |- (g:~P1 a-1-1-onto->~P1 b -> ({x} e. dom g <-> E.y{x}g{y}))
92		f1odm 5291	. . . . . . . . . . . . . 14 |- (g:~P1 a-1-1-onto->~P1 b -> dom g = ~P1 a)
93	92	eleq2d 2420	. . . . . . . . . . . . 13 |- (g:~P1 a-1-1-onto->~P1 b -> ({x} e. dom g <-> {x} e. ~P1 a))
94	91, 93	bitr3d 246	. . . . . . . . . . . 12 |- (g:~P1 a-1-1-onto->~P1 b -> (E.y{x}g{y} <-> {x} e. ~P1 a))
95		snelpw1 4147	. . . . . . . . . . . 12 |- ({x} e. ~P1 a <-> x e. a)
96	94, 95	syl6bb 252	. . . . . . . . . . 11 |- (g:~P1 a-1-1-onto->~P1 b -> (E.y{x}g{y} <-> x e. a))
97	96	eqabcdv 2470	. . . . . . . . . 10 |- (g:~P1 a-1-1-onto->~P1 b -> {x | E.y{x}g{y}} = a)
98	68, 97	syl5eq 2397	. . . . . . . . 9 |- (g:~P1 a-1-1-onto->~P1 b -> dom {<.x, y>. | {x}g{y}} = a)
99		df-fn 4791	. . . . . . . . 9 |- ({<.x, y>. | {x}g{y}} Fn a <-> (Fun {<.x, y>. | {x}g{y}} /\ dom {<.x, y>. | {x}g{y}} = a))
100	67, 98, 99	sylanbrc 645	. . . . . . . 8 |- (g:~P1 a-1-1-onto->~P1 b -> {<.x, y>. | {x}g{y}} Fn a)
101		f1ocnv 5300	. . . . . . . . . . . . . . 15 |- (g:~P1 a-1-1-onto->~P1 b -> `'g:~P1 b-1-1-onto->~P1 a)
102		f1ofun 5290	. . . . . . . . . . . . . . 15 |- (`'g:~P1 b-1-1-onto->~P1 a -> Fun `'g)
103		fununiq 5518	. . . . . . . . . . . . . . . . 17 |- ((Fun `'g /\ {y}`'g{x} /\ {y}`'g{z}) -> {x} = {z})
104	103	3expib 1154	. . . . . . . . . . . . . . . 16 |- (Fun `'g -> (({y}`'g{x} /\ {y}`'g{z}) -> {x} = {z}))
105		brcnv 4893	. . . . . . . . . . . . . . . . 17 |- ({y}`'g{x} <-> {x}g{y})
106		brcnv 4893	. . . . . . . . . . . . . . . . 17 |- ({y}`'g{z} <-> {z}g{y})
107	105, 106	anbi12i 678	. . . . . . . . . . . . . . . 16 |- (({y}`'g{x} /\ {y}`'g{z}) <-> ({x}g{y} /\ {z}g{y}))
108		vex 2863	. . . . . . . . . . . . . . . . 17 |- x e. _V
109	108	sneqb 3877	. . . . . . . . . . . . . . . 16 |- ({x} = {z} <-> x = z)
110	104, 107, 109	3imtr3g 260	. . . . . . . . . . . . . . 15 |- (Fun `'g -> (({x}g{y} /\ {z}g{y}) -> x = z))
111	101, 102, 110	3syl 18	. . . . . . . . . . . . . 14 |- (g:~P1 a-1-1-onto->~P1 b -> (({x}g{y} /\ {z}g{y}) -> x = z))
112	111	alrimivv 1632	. . . . . . . . . . . . 13 |- (g:~P1 a-1-1-onto->~P1 b -> A.xA.z(({x}g{y} /\ {z}g{y}) -> x = z))
113		sneq 3745	. . . . . . . . . . . . . . 15 |- (x = z -> {x} = {z})
114	113	breq1d 4650	. . . . . . . . . . . . . 14 |- (x = z -> ({x}g{y} <-> {z}g{y}))
115	114	mo4 2237	. . . . . . . . . . . . 13 |- (E*x{x}g{y} <-> A.xA.z(({x}g{y} /\ {z}g{y}) -> x = z))
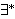116	112, 115	sylibr 203	. . . . . . . . . . . 12 |- (g:~P1 a-1-1-onto->~P1 b -> E*x{x}g{y})
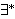117	116	alrimiv 1631	. . . . . . . . . . 11 |- (g:~P1 a-1-1-onto->~P1 b -> A.yE*x{x}g{y})
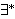118		funopab 5140	. . . . . . . . . . 11 |- (Fun {<.y, x>. | {x}g{y}} <-> A.yE*x{x}g{y})
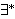119	117, 118	sylibr 203	. . . . . . . . . 10 |- (g:~P1 a-1-1-onto->~P1 b -> Fun {<.y, x>. | {x}g{y}})
120		dmopab 4916	. . . . . . . . . . 11 |- dom {<.y, x>. | {x}g{y}} = {y | E.x{x}g{y}}
121		elrn 4897	. . . . . . . . . . . . . . . 16 |- ({y} e. ran g <-> E.z zg{y})
122		breldm 4912	. . . . . . . . . . . . . . . . . 18 |- (zg{y} -> z e. dom g)
123	92	eleq2d 2420	. . . . . . . . . . . . . . . . . . . 20 |- (g:~P1 a-1-1-onto->~P1 b -> (z e. dom g <-> z e. ~P1 a))
124		elpw1 4145	. . . . . . . . . . . . . . . . . . . . 21 |- (z e. ~P1 a <-> E.w e. a z = {w})
125		breq1 4643	. . . . . . . . . . . . . . . . . . . . . . 23 |- (z = {w} -> (zg{y} <-> {w}g{y}))
126		sneq 3745	. . . . . . . . . . . . . . . . . . . . . . . . 25 |- (x = w -> {x} = {w})
127	126	breq1d 4650	. . . . . . . . . . . . . . . . . . . . . . . 24 |- (x = w -> ({x}g{y} <-> {w}g{y}))
128	77, 127	spcev 2947	. . . . . . . . . . . . . . . . . . . . . . 23 |- ({w}g{y} -> E.x{x}g{y})
129	125, 128	syl6bi 219	. . . . . . . . . . . . . . . . . . . . . 22 |- (z = {w} -> (zg{y} -> E.x{x}g{y}))
130	129	rexlimivw 2735	. . . . . . . . . . . . . . . . . . . . 21 |- (E.w e. a z = {w} -> (zg{y} -> E.x{x}g{y}))
131	124, 130	sylbi 187	. . . . . . . . . . . . . . . . . . . 20 |- (z e. ~P1 a -> (zg{y} -> E.x{x}g{y}))
132	123, 131	syl6bi 219	. . . . . . . . . . . . . . . . . . 19 |- (g:~P1 a-1-1-onto->~P1 b -> (z e. dom g -> (zg{y} -> E.x{x}g{y})))
133	132	com23 72	. . . . . . . . . . . . . . . . . 18 |- (g:~P1 a-1-1-onto->~P1 b -> (zg{y} -> (z e. dom g -> E.x{x}g{y})))
134	122, 133	mpdi 38	. . . . . . . . . . . . . . . . 17 |- (g:~P1 a-1-1-onto->~P1 b -> (zg{y} -> E.x{x}g{y}))
135	134	exlimdv 1636	. . . . . . . . . . . . . . . 16 |- (g:~P1 a-1-1-onto->~P1 b -> (E.z zg{y} -> E.x{x}g{y}))
136	121, 135	syl5bi 208	. . . . . . . . . . . . . . 15 |- (g:~P1 a-1-1-onto->~P1 b -> ({y} e. ran g -> E.x{x}g{y}))
137		brelrn 4961	. . . . . . . . . . . . . . . 16 |- ({x}g{y} -> {y} e. ran g)
138	137	exlimiv 1634	. . . . . . . . . . . . . . 15 |- (E.x{x}g{y} -> {y} e. ran g)
139	136, 138	impbid1 194	. . . . . . . . . . . . . 14 |- (g:~P1 a-1-1-onto->~P1 b -> ({y} e. ran g <-> E.x{x}g{y}))
140	73	eleq2d 2420	. . . . . . . . . . . . . 14 |- (g:~P1 a-1-1-onto->~P1 b -> ({y} e. ran g <-> {y} e. ~P1 b))
141	139, 140	bitr3d 246	. . . . . . . . . . . . 13 |- (g:~P1 a-1-1-onto->~P1 b -> (E.x{x}g{y} <-> {y} e. ~P1 b))
142		snelpw1 4147	. . . . . . . . . . . . 13 |- ({y} e. ~P1 b <-> y e. b)
143	141, 142	syl6bb 252	. . . . . . . . . . . 12 |- (g:~P1 a-1-1-onto->~P1 b -> (E.x{x}g{y} <-> y e. b))
144	143	eqabcdv 2470	. . . . . . . . . . 11 |- (g:~P1 a-1-1-onto->~P1 b -> {y | E.x{x}g{y}} = b)
145	120, 144	syl5eq 2397	. . . . . . . . . 10 |- (g:~P1 a-1-1-onto->~P1 b -> dom {<.y, x>. | {x}g{y}} = b)
146		df-fn 4791	. . . . . . . . . 10 |- ({<.y, x>. | {x}g{y}} Fn b <-> (Fun {<.y, x>. | {x}g{y}} /\ dom {<.y, x>. | {x}g{y}} = b))
147	119, 145, 146	sylanbrc 645	. . . . . . . . 9 |- (g:~P1 a-1-1-onto->~P1 b -> {<.y, x>. | {x}g{y}} Fn b)
148		cnvopab 5031	. . . . . . . . . 10 |- `'{<.x, y>. | {x}g{y}} = {<.y, x>. | {x}g{y}}
149	148	fneq1i 5179	. . . . . . . . 9 |- (`'{<.x, y>. | {x}g{y}} Fn b <-> {<.y, x>. | {x}g{y}} Fn b)
150	147, 149	sylibr 203	. . . . . . . 8 |- (g:~P1 a-1-1-onto->~P1 b -> `'{<.x, y>. | {x}g{y}} Fn b)
151		dff1o4 5295	. . . . . . . 8 |- ({<.x, y>. | {x}g{y}}:a-1-1-onto->b <-> ({<.x, y>. | {x}g{y}} Fn a /\ `'{<.x, y>. | {x}g{y}} Fn b))
152	100, 150, 151	sylanbrc 645	. . . . . . 7 |- (g:~P1 a-1-1-onto->~P1 b -> {<.x, y>. | {x}g{y}}:a-1-1-onto->b)
153		enpw1lem1 6062	. . . . . . . 8 |- {<.x, y>. | {x}g{y}} e. _V
154	153	f1oen 6034	. . . . . . 7 |- ({<.x, y>. | {x}g{y}}:a-1-1-onto->b -> a ~~ b)
155	152, 154	syl 15	. . . . . 6 |- (g:~P1 a-1-1-onto->~P1 b -> a ~~ b)
156	155	exlimiv 1634	. . . . 5 |- (E.g g:~P1 a-1-1-onto->~P1 b -> a ~~ b)
157	52, 156	sylbi 187	. . . 4 |- (~P1 a ~~ ~P1 b -> a ~~ b)
158	51, 157	impbii 180	. . 3 |- (a ~~ b <-> ~P1 a ~~ ~P1 b)
159	10, 14, 158	vtocl2g 2919	. 2 |- ((A e. _V /\ B e. _V) -> (A ~~ B <-> ~P1 A ~~ ~P1 B))
160	1, 6, 159	pm5.21nii 342	1 |- (A ~~ B <-> ~P1 A ~~ ~P1 B)

Syntax hints:   -> wi 4   <-> wb 176   /\ wa 358   /\ w3a 934  A.wal 1540  E.wex 1541   = wceq 1642   e. wcel 1710  E*wmo 2205  {cab 2339  E.wrex 2616  _Vcvv 2860  {csn 3738  ~P₁ cpw1 4136  {copab 4623   class class class wbr 4640   SI csi 4721  `'ccnv 4772  dom cdm 4773  ran crn 4774  Fun wfun 4776   Fn wfn 4777  -->wf 4778  -1-1->wf1 4779  -onto->wfo 4780  -1-1-onto->wf1o 4781   ~~ cen 6029

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1546  ax-5 1557  ax-17 1616  ax-9 1654  ax-8 1675  ax-13 1712  ax-14 1714  ax-6 1729  ax-7 1734  ax-11 1746  ax-12 1925  ax-ext 2334  ax-nin 4079  ax-xp 4080  ax-cnv 4081  ax-1c 4082  ax-sset 4083  ax-si 4084  ax-ins2 4085  ax-ins3 4086  ax-typlower 4087  ax-sn 4088

This theorem depends on definitions:  df-bi 177  df-or 359  df-an 360  df-3or 935  df-3an 936  df-nan 1288  df-tru 1319  df-ex 1542  df-nf 1545  df-sb 1649  df-eu 2208  df-mo 2209  df-clab 2340  df-cleq 2346  df-clel 2349  df-nfc 2479  df-ne 2519  df-ral 2620  df-rex 2621  df-reu 2622  df-rmo 2623  df-rab 2624  df-v 2862  df-sbc 3048  df-nin 3212  df-compl 3213  df-in 3214  df-un 3215  df-dif 3216  df-symdif 3217  df-ss 3260  df-pss 3262  df-nul 3552  df-if 3664  df-pw 3725  df-sn 3742  df-pr 3743  df-uni 3893  df-int 3928  df-opk 4059  df-1c 4137  df-pw1 4138  df-uni1 4139  df-xpk 4186  df-cnvk 4187  df-ins2k 4188  df-ins3k 4189  df-imak 4190  df-cok 4191  df-p6 4192  df-sik 4193  df-ssetk 4194  df-imagek 4195  df-idk 4196  df-iota 4340  df-0c 4378  df-addc 4379  df-nnc 4380  df-fin 4381  df-lefin 4441  df-ltfin 4442  df-ncfin 4443  df-tfin 4444  df-evenfin 4445  df-oddfin 4446  df-sfin 4447  df-spfin 4448  df-phi 4566  df-op 4567  df-proj1 4568  df-proj2 4569  df-opab 4624  df-br 4641  df-1st 4724  df-swap 4725  df-co 4727  df-ima 4728  df-si 4729  df-id 4768  df-cnv 4786  df-rn 4787  df-dm 4788  df-fun 4790  df-fn 4791  df-f 4792  df-f1 4793  df-fo 4794  df-f1o 4795  df-2nd 4798  df-en 6030

This theorem is referenced by:  ncpw1  6153  ce0addcnnul  6180  cenc  6182  tc11  6229