| Description: Inference from Theorem
19.23 of [Margaris] p. 90.
This inference, along with our many variants such as rexlimdv 2738, is
used to implement a metatheorem called "Rule C" that is given
in many
logic textbooks. See, for example, Rule C in [Mendelson] p. 81, Rule C
in [Margaris] p. 40, or Rule C in Hirst
and Hirst's A Primer for Logic
and Proof p. 59 (PDF p. 65) at
http://www.mathsci.appstate.edu/~hirstjl/primer/hirst.pdf 2738.
In informal proofs, the statement "Let  be an element such that..."
almost always means an implicit application of Rule C. be an element such that..."
almost always means an implicit application of Rule C.
In essence, Rule C states that if we can prove that some element  exists satisfying a wff, i.e.
exists satisfying a wff, i.e. 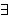   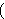  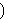 where where  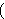  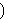 has has
 free, then we
can use free, then we
can use  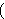  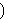 as a hypothesis for the proof
where as a hypothesis for the proof
where  is a
new (ficticious) constant not appearing previously in
the proof, nor in any axioms used, nor in the theorem to be proved. The
purpose of Rule C is to get rid of the existential quantifier. is a
new (ficticious) constant not appearing previously in
the proof, nor in any axioms used, nor in the theorem to be proved. The
purpose of Rule C is to get rid of the existential quantifier.
We cannot do this in Metamath directly. Instead, we use the original
 (containing
(containing  ) as an
antecedent for the main part of the
proof. We eventually arrive at ) as an
antecedent for the main part of the
proof. We eventually arrive at 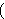  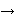  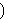 where where  is the
theorem to be proved and does not contain is the
theorem to be proved and does not contain  . Then we apply
exlimiv 1634 to arrive at . Then we apply
exlimiv 1634 to arrive at 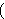 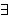   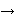  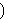 . Finally, we separately
prove . Finally, we separately
prove 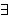   and detach it with modus ponens ax-mp 5
to arrive at
the final theorem and detach it with modus ponens ax-mp 5
to arrive at
the final theorem  . (Contributed by NM, 5-Aug-1993.) (Revised
by Wolf Lammen to remove dependency on ax-9 and ax-8,
4-Dec-2017.) . (Contributed by NM, 5-Aug-1993.) (Revised
by Wolf Lammen to remove dependency on ax-9 and ax-8,
4-Dec-2017.) |