| Description: Russell's Paradox.
Proposition 4.14 of [TakeutiZaring] p.
14.
In the late 1800s, Frege's Axiom of (unrestricted) Comprehension,
expressed in our notation as   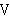 , asserted that any
collection
of sets , asserted that any
collection
of sets  is a
set i.e. belongs to the universe is a
set i.e. belongs to the universe 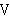 of all sets.
In particular, by substituting of all sets.
In particular, by substituting 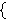 
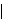  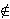  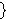 (the
"Russell class")
for (the
"Russell class")
for  , it
asserted , it
asserted 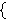  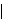  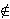  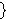  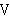 , meaning that the
"collection of all sets which are not members of themselves"
is a set.
However, here we prove , meaning that the
"collection of all sets which are not members of themselves"
is a set.
However, here we prove 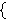  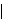  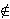  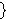 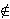 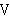 . This contradiction
was discovered by Russell in 1901 (published in 1903), invalidating the
Comprehension Axiom and leading to the collapse of Frege's system. . This contradiction
was discovered by Russell in 1901 (published in 1903), invalidating the
Comprehension Axiom and leading to the collapse of Frege's system.
In 1908, Zermelo rectified this fatal flaw by replacing Comprehension
with a weaker Subset (or Separation) Axiom asserting that  is a set
only when it is smaller than some other set is a set
only when it is smaller than some other set 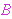 . The intuitionistic
set theory IZF includes such a separation axiom, Axiom 6 of [Crosilla]
p. "Axioms of CZF and IZF", which we include as ax-sep 4178.
(Contributed by NM, 7-Aug-1994.) . The intuitionistic
set theory IZF includes such a separation axiom, Axiom 6 of [Crosilla]
p. "Axioms of CZF and IZF", which we include as ax-sep 4178.
(Contributed by NM, 7-Aug-1994.) |