Description: Two ways to say
" is a set":
A class is a set":
A class  is a member
of the
universal class is a member
of the
universal class 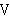 (see df-v 2778) if and only if the class (see df-v 2778) if and only if the class  exists (i.e. there exists some set
exists (i.e. there exists some set  equal to class equal to class  ).
Theorem 6.9 of [Quine] p. 43.
Notational convention: We will use the
notational device " ).
Theorem 6.9 of [Quine] p. 43.
Notational convention: We will use the
notational device "  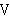 " to mean
" " to mean
" is a set"
very
frequently, for example in uniex 4502. Note the when is a set"
very
frequently, for example in uniex 4502. Note the when  is not a set,
it is called a proper class. In some theorems, such as uniexg 4504, in
order to shorten certain proofs we use the more general antecedent is not a set,
it is called a proper class. In some theorems, such as uniexg 4504, in
order to shorten certain proofs we use the more general antecedent
  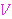 instead of instead of   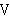 to
mean " to
mean " is a
set." is a
set."
Note that a constant is implicitly considered distinct from all
variables. This is why 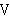 is not included in the distinct variable
list, even though df-clel 2203 requires that the expression substituted for is not included in the distinct variable
list, even though df-clel 2203 requires that the expression substituted for
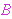 not contain not contain
 . (Also, the Metamath
spec does not allow
constants in the distinct variable list.) (Contributed by NM,
26-May-1993.) . (Also, the Metamath
spec does not allow
constants in the distinct variable list.) (Contributed by NM,
26-May-1993.) |