xpassen - New Foundations Explorer

	New Foundations Explorer		< Previous Next > Nearby theorems
Mirrors > Home > NFE Home > Th. List > xpassen		Unicode version

Theorem xpassen 6058

Description: Associative law for equinumerosity of cross product. Proposition 4.22(e) of [Mendelson] p. 254. (Contributed by SF, 24-Feb-2015.)

**Hypotheses**
Ref	Expression
xpassen.1
xpassen.2
xpassen.3

**Assertion**
Ref	Expression
xpassen

Proof of Theorem xpassen Dummy variables

are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		1stfo 5506	. . . . . . . . . . 11
2		fof 5270	. . . . . . . . . . 11
3	1, 2	ax-mp 5	. . . . . . . . . 10
4		dffn2 5225	. . . . . . . . . 10
5	3, 4	mpbir 200	. . . . . . . . 9
6		ssv 3292	. . . . . . . . 9
7		fnco 5192	. . . . . . . . 9 $/\$ $/\$
8	5, 5, 6, 7	mp3an 1277	. . . . . . . 8
9		2ndfo 5507	. . . . . . . . . . . 12
10		fofn 5272	. . . . . . . . . . . 12
11	9, 10	ax-mp 5	. . . . . . . . . . 11
12		fnco 5192	. . . . . . . . . . 11 $/\$ $/\$
13	11, 5, 6, 12	mp3an 1277	. . . . . . . . . 10
14		fntxp 5805	. . . . . . . . . 10 $/\$
15	13, 11, 14	mp2an 653	. . . . . . . . 9
16		inidm 3465	. . . . . . . . . 10
17	16	fneq2i 5180	. . . . . . . . 9
18	15, 17	mpbi 199	. . . . . . . 8
19		fntxp 5805	. . . . . . . 8 $/\$
20	8, 18, 19	mp2an 653	. . . . . . 7
21	16	fneq2i 5180	. . . . . . 7
22	20, 21	mpbi 199	. . . . . 6
23		dffn2 5225	. . . . . 6
24	22, 23	mpbi 199	. . . . 5
25		xpassenlem 6057	. . . . . . . . 9 Proj1 Proj1 Proj1 $/\$ Proj2 Proj1 Proj1 Proj2 $/\$ Proj2 Proj2 Proj2
26		xpassenlem 6057	. . . . . . . . 9 Proj1 Proj1 Proj1 $/\$ Proj2 Proj1 Proj1 Proj2 $/\$ Proj2 Proj2 Proj2
27		simp1 955	. . . . . . . . . . . . . 14 Proj1 Proj1 Proj1 $/\$ Proj2 Proj1 Proj1 Proj2 $/\$ Proj2 Proj2 Proj2 Proj1 Proj1 Proj1
28		simp1 955	. . . . . . . . . . . . . 14 Proj1 Proj1 Proj1 $/\$ Proj2 Proj1 Proj1 Proj2 $/\$ Proj2 Proj2 Proj2 Proj1 Proj1 Proj1
29		eqtr3 2372	. . . . . . . . . . . . . 14 Proj1 Proj1 Proj1 $/\$ Proj1 Proj1 Proj1 Proj1 Proj1 Proj1 Proj1
30	27, 28, 29	syl2an 463	. . . . . . . . . . . . 13 Proj1 Proj1 Proj1 $/\$ Proj2 Proj1 Proj1 Proj2 $/\$ Proj2 Proj2 Proj2 $/\$ Proj1 Proj1 Proj1 $/\$ Proj2 Proj1 Proj1 Proj2 $/\$ Proj2 Proj2 Proj2 Proj1 Proj1 Proj1 Proj1
31		simp2 956	. . . . . . . . . . . . . 14 Proj1 Proj1 Proj1 $/\$ Proj2 Proj1 Proj1 Proj2 $/\$ Proj2 Proj2 Proj2 Proj2 Proj1 Proj1 Proj2
32		simp2 956	. . . . . . . . . . . . . 14 Proj1 Proj1 Proj1 $/\$ Proj2 Proj1 Proj1 Proj2 $/\$ Proj2 Proj2 Proj2 Proj2 Proj1 Proj1 Proj2
33		eqtr3 2372	. . . . . . . . . . . . . 14 Proj2 Proj1 Proj1 Proj2 $/\$ Proj2 Proj1 Proj1 Proj2 Proj2 Proj1 Proj2 Proj1
34	31, 32, 33	syl2an 463	. . . . . . . . . . . . 13 Proj1 Proj1 Proj1 $/\$ Proj2 Proj1 Proj1 Proj2 $/\$ Proj2 Proj2 Proj2 $/\$ Proj1 Proj1 Proj1 $/\$ Proj2 Proj1 Proj1 Proj2 $/\$ Proj2 Proj2 Proj2 Proj2 Proj1 Proj2 Proj1
35	30, 34	opeq12d 4587	. . . . . . . . . . . 12 Proj1 Proj1 Proj1 $/\$ Proj2 Proj1 Proj1 Proj2 $/\$ Proj2 Proj2 Proj2 $/\$ Proj1 Proj1 Proj1 $/\$ Proj2 Proj1 Proj1 Proj2 $/\$ Proj2 Proj2 Proj2 Proj1 Proj1 Proj2 Proj1 Proj1 Proj1 Proj2 Proj1
36		opeq 4620	. . . . . . . . . . . 12 Proj1 Proj1 Proj1 Proj2 Proj1
37		opeq 4620	. . . . . . . . . . . 12 Proj1 Proj1 Proj1 Proj2 Proj1
38	35, 36, 37	3eqtr4g 2410	. . . . . . . . . . 11 Proj1 Proj1 Proj1 $/\$ Proj2 Proj1 Proj1 Proj2 $/\$ Proj2 Proj2 Proj2 $/\$ Proj1 Proj1 Proj1 $/\$ Proj2 Proj1 Proj1 Proj2 $/\$ Proj2 Proj2 Proj2 Proj1 Proj1
39		simp3 957	. . . . . . . . . . . 12 Proj1 Proj1 Proj1 $/\$ Proj2 Proj1 Proj1 Proj2 $/\$ Proj2 Proj2 Proj2 Proj2 Proj2 Proj2
40		simp3 957	. . . . . . . . . . . 12 Proj1 Proj1 Proj1 $/\$ Proj2 Proj1 Proj1 Proj2 $/\$ Proj2 Proj2 Proj2 Proj2 Proj2 Proj2
41		eqtr3 2372	. . . . . . . . . . . 12 Proj2 Proj2 Proj2 $/\$ Proj2 Proj2 Proj2 Proj2 Proj2
42	39, 40, 41	syl2an 463	. . . . . . . . . . 11 Proj1 Proj1 Proj1 $/\$ Proj2 Proj1 Proj1 Proj2 $/\$ Proj2 Proj2 Proj2 $/\$ Proj1 Proj1 Proj1 $/\$ Proj2 Proj1 Proj1 Proj2 $/\$ Proj2 Proj2 Proj2 Proj2 Proj2
43	38, 42	opeq12d 4587	. . . . . . . . . 10 Proj1 Proj1 Proj1 $/\$ Proj2 Proj1 Proj1 Proj2 $/\$ Proj2 Proj2 Proj2 $/\$ Proj1 Proj1 Proj1 $/\$ Proj2 Proj1 Proj1 Proj2 $/\$ Proj2 Proj2 Proj2 Proj1 Proj2 Proj1 Proj2
44		opeq 4620	. . . . . . . . . 10 Proj1 Proj2
45		opeq 4620	. . . . . . . . . 10 Proj1 Proj2
46	43, 44, 45	3eqtr4g 2410	. . . . . . . . 9 Proj1 Proj1 Proj1 $/\$ Proj2 Proj1 Proj1 Proj2 $/\$ Proj2 Proj2 Proj2 $/\$ Proj1 Proj1 Proj1 $/\$ Proj2 Proj1 Proj1 Proj2 $/\$ Proj2 Proj2 Proj2
47	25, 26, 46	syl2anb 465	. . . . . . . 8 $/\$
48	47	gen2 1547	. . . . . . 7 $/\$
49		breq1 4643	. . . . . . . 8
50	49	mo4 2237	. . . . . . 7 $/\$
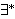51	48, 50	mpbir 200	. . . . . 6
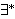
52	51	ax-gen 1546	. . . . 5
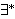
53		dff12 5258	. . . . 5 $/\$
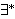54	24, 52, 53	mpbir2an 886	. . . 4
55		ssv 3292	. . . 4
56		f1ores 5301	. . . 4 $/\$
57	54, 55, 56	mp2an 653	. . 3
58		vex 2863	. . . . . 6
59		opeqex 4622	. . . . . 6
60		rexcom4 2879	. . . . . . . . . . . 12 $/\$ $/\$
61		rexcom4 2879	. . . . . . . . . . . . . 14 $/\$ $/\$
62		rexcom4 2879	. . . . . . . . . . . . . . . 16 $/\$ $/\$
63		vex 2863	. . . . . . . . . . . . . . . . . . . . 21
64		vex 2863	. . . . . . . . . . . . . . . . . . . . 21
65	63, 64	opex 4589	. . . . . . . . . . . . . . . . . . . 20
66		vex 2863	. . . . . . . . . . . . . . . . . . . 20
67	65, 66	opex 4589	. . . . . . . . . . . . . . . . . . 19
68		breq1 4643	. . . . . . . . . . . . . . . . . . 19
69	67, 68	ceqsexv 2895	. . . . . . . . . . . . . . . . . 18 $/\$
70	65, 66	brco1st 5778	. . . . . . . . . . . . . . . . . . . . 21
71	63, 64	opbr1st 5502	. . . . . . . . . . . . . . . . . . . . 21
72	70, 71	bitri 240	. . . . . . . . . . . . . . . . . . . 20
73		trtxp 5782	. . . . . . . . . . . . . . . . . . . . 21 $/\$
74		brco 4884	. . . . . . . . . . . . . . . . . . . . . . 23 $/\$
75	65, 66	opbr1st 5502	. . . . . . . . . . . . . . . . . . . . . . . . . 26
76		eqcom 2355	. . . . . . . . . . . . . . . . . . . . . . . . . 26
77	75, 76	bitri 240	. . . . . . . . . . . . . . . . . . . . . . . . 25
78	77	anbi1i 676	. . . . . . . . . . . . . . . . . . . . . . . 24 $/\$ $/\$
79	78	exbii 1582	. . . . . . . . . . . . . . . . . . . . . . 23 $/\$ $/\$
80		breq1 4643	. . . . . . . . . . . . . . . . . . . . . . . . 25
81	65, 80	ceqsexv 2895	. . . . . . . . . . . . . . . . . . . . . . . 24 $/\$
82	63, 64	opbr2nd 5503	. . . . . . . . . . . . . . . . . . . . . . . 24
83	81, 82	bitri 240	. . . . . . . . . . . . . . . . . . . . . . 23 $/\$
84	74, 79, 83	3bitri 262	. . . . . . . . . . . . . . . . . . . . . 22
85	65, 66	opbr2nd 5503	. . . . . . . . . . . . . . . . . . . . . 22
86	84, 85	anbi12i 678	. . . . . . . . . . . . . . . . . . . . 21 $/\$ $/\$
87	73, 86	bitri 240	. . . . . . . . . . . . . . . . . . . 20 $/\$
88	72, 87	anbi12i 678	. . . . . . . . . . . . . . . . . . 19 $/\$ $/\$ $/\$
89		trtxp 5782	. . . . . . . . . . . . . . . . . . 19 $/\$
90		3anass 938	. . . . . . . . . . . . . . . . . . 19 $/\$ $/\$ $/\$ $/\$
91	88, 89, 90	3bitr4i 268	. . . . . . . . . . . . . . . . . 18 $/\$ $/\$
92	69, 91	bitri 240	. . . . . . . . . . . . . . . . 17 $/\$ $/\$ $/\$
93	92	rexbii 2640	. . . . . . . . . . . . . . . 16 $/\$ $/\$ $/\$
94	62, 93	bitr3i 242	. . . . . . . . . . . . . . 15 $/\$ $/\$ $/\$
95	94	rexbii 2640	. . . . . . . . . . . . . 14 $/\$ $/\$ $/\$
96	61, 95	bitr3i 242	. . . . . . . . . . . . 13 $/\$ $/\$ $/\$
97	96	rexbii 2640	. . . . . . . . . . . 12 $/\$ $/\$ $/\$
98	60, 97	bitr3i 242	. . . . . . . . . . 11 $/\$ $/\$ $/\$
99		3reeanv 2780	. . . . . . . . . . 11 $/\$ $/\$ $/\$ $/\$
100	98, 99	bitri 240	. . . . . . . . . 10 $/\$ $/\$ $/\$
101		r19.41v 2765	. . . . . . . . . . . 12 $/\$ $/\$
102		r19.41v 2765	. . . . . . . . . . . . . . 15 $/\$ $/\$
103	102	rexbii 2640	. . . . . . . . . . . . . 14 $/\$ $/\$
104		r19.41v 2765	. . . . . . . . . . . . . 14 $/\$ $/\$
105	103, 104	bitri 240	. . . . . . . . . . . . 13 $/\$ $/\$
106	105	rexbii 2640	. . . . . . . . . . . 12 $/\$ $/\$
107		elxp2 4803	. . . . . . . . . . . . . 14
108		df-rex 2621	. . . . . . . . . . . . . 14 $/\$
109		rexcom4 2879	. . . . . . . . . . . . . . 15 $/\$ $/\$
110		opeq1 4579	. . . . . . . . . . . . . . . . . . . . . 22
111	110	eqeq2d 2364	. . . . . . . . . . . . . . . . . . . . 21
112	65, 111	ceqsexv 2895	. . . . . . . . . . . . . . . . . . . 20 $/\$
113	112	rexbii 2640	. . . . . . . . . . . . . . . . . . 19 $/\$
114		rexcom4 2879	. . . . . . . . . . . . . . . . . . 19 $/\$ $/\$
115	113, 114	bitr3i 242	. . . . . . . . . . . . . . . . . 18 $/\$
116	115	rexbii 2640	. . . . . . . . . . . . . . . . 17 $/\$
117		rexcom4 2879	. . . . . . . . . . . . . . . . 17 $/\$ $/\$
118	116, 117	bitri 240	. . . . . . . . . . . . . . . 16 $/\$
119	118	rexbii 2640	. . . . . . . . . . . . . . 15 $/\$
120		r19.41v 2765	. . . . . . . . . . . . . . . . 17 $/\$ $/\$
121		reeanv 2779	. . . . . . . . . . . . . . . . . 18 $/\$ $/\$
122	121	rexbii 2640	. . . . . . . . . . . . . . . . 17 $/\$ $/\$
123		elxp2 4803	. . . . . . . . . . . . . . . . . 18
124	123	anbi1i 676	. . . . . . . . . . . . . . . . 17 $/\$ $/\$
125	120, 122, 124	3bitr4ri 269	. . . . . . . . . . . . . . . 16 $/\$ $/\$
126	125	exbii 1582	. . . . . . . . . . . . . . 15 $/\$ $/\$
127	109, 119, 126	3bitr4ri 269	. . . . . . . . . . . . . 14 $/\$
128	107, 108, 127	3bitri 262	. . . . . . . . . . . . 13
129	128	anbi1i 676	. . . . . . . . . . . 12 $/\$ $/\$
130	101, 106, 129	3bitr4ri 269	. . . . . . . . . . 11 $/\$ $/\$
131	130	exbii 1582	. . . . . . . . . 10 $/\$ $/\$
132		risset 2662	. . . . . . . . . . 11
133		risset 2662	. . . . . . . . . . 11
134		risset 2662	. . . . . . . . . . 11
135	132, 133, 134	3anbi123i 1140	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$
136	100, 131, 135	3bitr4i 268	. . . . . . . . 9 $/\$ $/\$ $/\$
137		elima2 4756	. . . . . . . . 9 $/\$
138		opelxp 4812	. . . . . . . . . . 11 $/\$
139	138	anbi2i 675	. . . . . . . . . 10 $/\$ $/\$ $/\$
140		opelxp 4812	. . . . . . . . . 10 $/\$
141		3anass 938	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$
142	139, 140, 141	3bitr4i 268	. . . . . . . . 9 $/\$ $/\$
143	136, 137, 142	3bitr4i 268	. . . . . . . 8
144		opeq2 4580	. . . . . . . . . 10
145	144	eleq1d 2419	. . . . . . . . 9
146	144	eleq1d 2419	. . . . . . . . 9
147	145, 146	bibi12d 312	. . . . . . . 8
148	143, 147	mpbiri 224	. . . . . . 7
149	148	exlimivv 1635	. . . . . 6
150	58, 59, 149	mp2b 9	. . . . 5
151	150	eqrelriv 4851	. . . 4
152		f1oeq3 5284	. . . 4
153	151, 152	ax-mp 5	. . 3
154	57, 153	mpbi 199	. 2
155		1stex 4740	. . . . . 6
156	155, 155	coex 4751	. . . . 5
157		2ndex 5113	. . . . . . 7
158	157, 155	coex 4751	. . . . . 6
159	158, 157	txpex 5786	. . . . 5
160	156, 159	txpex 5786	. . . 4
161		xpassen.1	. . . . . 6
162		xpassen.2	. . . . . 6
163	161, 162	xpex 5116	. . . . 5
164		xpassen.3	. . . . 5
165	163, 164	xpex 5116	. . . 4
166	160, 165	resex 5118	. . 3
167	166	f1oen 6034	. 2
168	154, 167	ax-mp 5	1

Colors of variables: wff setvar class

Syntax hints:

wi 4

wb 176 $/\$ wa 358 $/\$ w3a 934

wal 1540

wex 1541

wceq 1642

wcel 1710

wmo 2205

wrex 2616

cvv 2860

cin 3209

wss 3258

cop 4562 Proj1 cproj1 4564 Proj2 cproj2 4565 class class class wbr 4640

c1st 4718

ccom 4722

cima 4723

cxp 4771

crn 4774

cres 4775

wfn 4777

wf 4778

wf1 4779

wfo 4780

wf1o 4781

c2nd 4784

ctxp 5736

cen 6029

This theorem was proved from axioms: ax-mp 5 ax-1 6 ax-2 7 ax-3 8 ax-gen 1546 ax-5 1557 ax-17 1616 ax-9 1654 ax-8 1675 ax-13 1712 ax-14 1714 ax-6 1729 ax-7 1734 ax-11 1746 ax-12 1925 ax-ext 2334 ax-nin 4079 ax-xp 4080 ax-cnv 4081 ax-1c 4082 ax-sset 4083 ax-si 4084 ax-ins2 4085 ax-ins3 4086 ax-typlower 4087 ax-sn 4088

This theorem depends on definitions: df-bi 177 df-or 359 df-an 360 df-3or 935 df-3an 936 df-nan 1288 df-tru 1319 df-ex 1542 df-nf 1545 df-sb 1649 df-eu 2208 df-mo 2209 df-clab 2340 df-cleq 2346 df-clel 2349 df-nfc 2479 df-ne 2519 df-ral 2620 df-rex 2621 df-reu 2622 df-rmo 2623 df-rab 2624 df-v 2862 df-sbc 3048 df-nin 3212 df-compl 3213 df-in 3214 df-un 3215 df-dif 3216 df-symdif 3217 df-ss 3260 df-pss 3262 df-nul 3552 df-if 3664 df-pw 3725 df-sn 3742 df-pr 3743 df-uni 3893 df-int 3928 df-opk 4059 df-1c 4137 df-pw1 4138 df-uni1 4139 df-xpk 4186 df-cnvk 4187 df-ins2k 4188 df-ins3k 4189 df-imak 4190 df-cok 4191 df-p6 4192 df-sik 4193 df-ssetk 4194 df-imagek 4195 df-idk 4196 df-iota 4340 df-0c 4378 df-addc 4379 df-nnc 4380 df-fin 4381 df-lefin 4441 df-ltfin 4442 df-ncfin 4443 df-tfin 4444 df-evenfin 4445 df-oddfin 4446 df-sfin 4447 df-spfin 4448 df-phi 4566 df-op 4567 df-proj1 4568 df-proj2 4569 df-opab 4624 df-br 4641 df-1st 4724 df-swap 4725 df-co 4727 df-ima 4728 df-id 4768 df-xp 4785 df-cnv 4786 df-rn 4787 df-dm 4788 df-res 4789 df-fun 4790 df-fn 4791 df-f 4792 df-f1 4793 df-fo 4794 df-f1o 4795 df-2nd 4798 df-txp 5737 df-en 6030

This theorem is referenced by: mucass 6136

W3C validator