Description: Define the value of a
function,      ,
also known as function
application. For example, ,
also known as function
application. For example,        . Typically,
function . Typically,
function  is
defined using maps-to notation (see df-mpt 4147), but
this is not required. For example, is
defined using maps-to notation (see df-mpt 4147), but
this is not required. For example,
            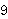   
      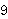 . We will later
define two-argument functions using ordered pairs as . We will later
define two-argument functions using ordered pairs as
               . This
particular definition is
quite convenient: it can be applied to any class and evaluates to the
empty set when it is not meaningful. The left apostrophe notation
originated with Peano and was adopted in Definition *30.01 of
[WhiteheadRussell] p. 235,
Definition 10.11 of [Quine] p. 68, and
Definition 6.11 of [TakeutiZaring]
p. 26. It means the same thing as
the more familiar . This
particular definition is
quite convenient: it can be applied to any class and evaluates to the
empty set when it is not meaningful. The left apostrophe notation
originated with Peano and was adopted in Definition *30.01 of
[WhiteheadRussell] p. 235,
Definition 10.11 of [Quine] p. 68, and
Definition 6.11 of [TakeutiZaring]
p. 26. It means the same thing as
the more familiar     notation for a function's value at notation for a function's value at  ,
i.e., " ,
i.e., " of of
 ," but without
context-dependent notational
ambiguity. (Contributed by NM, 1-Aug-1994.) Revised to use ," but without
context-dependent notational
ambiguity. (Contributed by NM, 1-Aug-1994.) Revised to use  .
(Revised by Scott Fenton, 6-Oct-2017.) .
(Revised by Scott Fenton, 6-Oct-2017.) |