| Step | Hyp | Ref
| Expression |
|---|
| 1 | | zfregfr 4666 |
. 2
  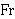  |
| 2 | | epel 4383 |
. . . . . 6
     
    |
| 3 | | epel 4383 |
. . . . . 6
     
    |
| 4 | 2, 3 | anbi12i 460 |
. . . . 5
        
         
   |
| 5 | | simpr 110 |
. . . . . 6
        
   
   
   
                 |
| 6 | | elirr 4633 |
. . . . . . . 8
         |
| 7 | | simprr 531 |
. . . . . . . . . 10
        
   
   
   
           |
| 8 | | noel 3495 |
. . . . . . . . . . . . 13
     |
| 9 | | eleq2 2293 |
. . . . . . . . . . . . 13
    
     
     |
| 10 | 8, 9 | mtbiri 679 |
. . . . . . . . . . . 12
    
      |
| 11 | | simprl 529 |
. . . . . . . . . . . 12
        
   
   
   
           |
| 12 | 10, 11 | nsyl3 629 |
. . . . . . . . . . 11
        
   
   
   
        
   |
| 13 | | elrabi 2956 |
. . . . . . . . . . . . . . . 16
                       
                  |
| 14 | | reg3exmidlemwe.a |
. . . . . . . . . . . . . . . 16
                              |
| 15 | 13, 14 | eleq2s 2324 |
. . . . . . . . . . . . . . 15
                |
| 16 | | elpri 3689 |
. . . . . . . . . . . . . . 15
                        |
| 17 | 15, 16 | syl 14 |
. . . . . . . . . . . . . 14
                  |
| 18 | 17 | orcomd 734 |
. . . . . . . . . . . . 13
                  |
| 19 | 18 | 3ad2ant2 1043 |
. . . . . . . . . . . 12
        
   
               |
| 20 | 19 | adantr 276 |
. . . . . . . . . . 11
        
   
   
   
                   |
| 21 | 12, 20 | ecased 1383 |
. . . . . . . . . 10
        
   
   
   
             |
| 22 | | noel 3495 |
. . . . . . . . . . . . 13
     |
| 23 | | eleq2 2293 |
. . . . . . . . . . . . 13
    
     
     |
| 24 | 22, 23 | mtbiri 679 |
. . . . . . . . . . . 12
    
      |
| 25 | 24, 7 | nsyl3 629 |
. . . . . . . . . . 11
        
   
   
   
        
   |
| 26 | | elrabi 2956 |
. . . . . . . . . . . . . . . 16
                       
                  |
| 27 | 26, 14 | eleq2s 2324 |
. . . . . . . . . . . . . . 15
                |
| 28 | | vex 2802 |
. . . . . . . . . . . . . . . 16
    |
| 29 | 28 | elpr 3687 |
. . . . . . . . . . . . . . 15
           
            |
| 30 | 27, 29 | sylib 122 |
. . . . . . . . . . . . . 14
                  |
| 31 | 30 | orcomd 734 |
. . . . . . . . . . . . 13
                  |
| 32 | 31 | 3ad2ant3 1044 |
. . . . . . . . . . . 12
        
   
               |
| 33 | 32 | adantr 276 |
. . . . . . . . . . 11
        
   
   
   
                   |
| 34 | 25, 33 | ecased 1383 |
. . . . . . . . . 10
        
   
   
   
             |
| 35 | 7, 21, 34 | 3eltr3d 2312 |
. . . . . . . . 9
        
   
   
   
               |
| 36 | 35 | ex 115 |
. . . . . . . 8
        
   
                       |
| 37 | 6, 36 | mtoi 668 |
. . . . . . 7
        
   
              |
| 38 | 37 | adantr 276 |
. . . . . 6
        
   
   
   
                  |
| 39 | 5, 38 | pm2.21dd 623 |
. . . . 5
        
   
   
   
           |
| 40 | 4, 39 | sylan2b 287 |
. . . 4
        
   
   
   
           |
| 41 | 40 | ex 115 |
. . 3
        
   
                   |
| 42 | 41 | rgen3 2617 |
. 2
    
   
   
       
       |
| 43 | | df-wetr 4425 |
. 2
   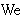  
  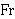 
    
   
   
       
         |
| 44 | 1, 42, 43 | mpbir2an 948 |
1
  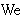  |