Proof of Theorem lidlrsppropdg
| Step | Hyp | Ref
| Expression |
|---|
| 1 | | lidlpropd.1 |
. . . . 5
            |
| 2 | | lidlpropdg.k |
. . . . . 6
        |
| 3 | | rlmbasg 14427 |
. . . . . 6
                ringLMod ringLMod     |
| 4 | 2, 3 | syl 14 |
. . . . 5
              ringLMod ringLMod     |
| 5 | 1, 4 | eqtrd 2262 |
. . . 4
          ringLMod ringLMod     |
| 6 | | lidlpropd.2 |
. . . . 5
            |
| 7 | | lidlpropdg.l |
. . . . . 6
        |
| 8 | | rlmbasg 14427 |
. . . . . 6
                ringLMod ringLMod     |
| 9 | 7, 8 | syl 14 |
. . . . 5
              ringLMod ringLMod     |
| 10 | 6, 9 | eqtrd 2262 |
. . . 4
          ringLMod ringLMod     |
| 11 | | lidlpropd.3 |
. . . 4
     
  |
| 12 | | lidlpropd.4 |
. . . . 5
    
   
                           |
| 13 | | rlmplusgg 14428 |
. . . . . . 7
                ringLMod ringLMod     |
| 14 | 2, 13 | syl 14 |
. . . . . 6
              ringLMod ringLMod     |
| 15 | 14 | oveqdr 6035 |
. . . . 5
    
   
                       ringLMod ringLMod       |
| 16 | | rlmplusgg 14428 |
. . . . . . 7
                ringLMod ringLMod     |
| 17 | 7, 16 | syl 14 |
. . . . . 6
              ringLMod ringLMod     |
| 18 | 17 | oveqdr 6035 |
. . . . 5
    
   
                       ringLMod ringLMod       |
| 19 | 12, 15, 18 | 3eqtr3d 2270 |
. . . 4
    
   
             ringLMod ringLMod             ringLMod ringLMod       |
| 20 | | rlmvscag 14433 |
. . . . . . 7
                ringLMod ringLMod     |
| 21 | 2, 20 | syl 14 |
. . . . . 6
              ringLMod ringLMod     |
| 22 | 21 | oveqdr 6035 |
. . . . 5
    
   
                       ringLMod ringLMod       |
| 23 | | lidlpropd.5 |
. . . . 5
    
   
                   |
| 24 | 22, 23 | eqeltrrd 2307 |
. . . 4
    
   
             ringLMod ringLMod         |
| 25 | | lidlpropd.6 |
. . . . 5
    
   
                           |
| 26 | | rlmvscag 14433 |
. . . . . . 7
                ringLMod ringLMod     |
| 27 | 7, 26 | syl 14 |
. . . . . 6
              ringLMod ringLMod     |
| 28 | 27 | oveqdr 6035 |
. . . . 5
    
   
                       ringLMod ringLMod       |
| 29 | 25, 22, 28 | 3eqtr3d 2270 |
. . . 4
    
   
             ringLMod ringLMod             ringLMod ringLMod       |
| 30 | | rlmscabas 14432 |
. . . . . 6
                Scalar Scalar  ringLMod ringLMod      |
| 31 | 2, 30 | syl 14 |
. . . . 5
              Scalar Scalar  ringLMod ringLMod      |
| 32 | 1, 31 | eqtrd 2262 |
. . . 4
          Scalar Scalar  ringLMod ringLMod      |
| 33 | | rlmscabas 14432 |
. . . . . 6
                Scalar Scalar  ringLMod ringLMod      |
| 34 | 7, 33 | syl 14 |
. . . . 5
              Scalar Scalar  ringLMod ringLMod      |
| 35 | 6, 34 | eqtrd 2262 |
. . . 4
          Scalar Scalar  ringLMod ringLMod      |
| 36 | | rlmfn 14425 |
. . . . 5
 ringLMod ringLMod   |
| 37 | 2 | elexd 2813 |
. . . . 5
        |
| 38 | | funfvex 5646 |
. . . . . 6
    ringLMod ringLMod     ringLMod ringLMod   ringLMod ringLMod      |
| 39 | 38 | funfni 5423 |
. . . . 5
   ringLMod ringLMod          ringLMod ringLMod      |
| 40 | 36, 37, 39 | sylancr 414 |
. . . 4
     ringLMod ringLMod      |
| 41 | 7 | elexd 2813 |
. . . . 5
        |
| 42 | | funfvex 5646 |
. . . . . 6
    ringLMod ringLMod     ringLMod ringLMod   ringLMod ringLMod      |
| 43 | 42 | funfni 5423 |
. . . . 5
   ringLMod ringLMod          ringLMod ringLMod      |
| 44 | 36, 41, 43 | sylancr 414 |
. . . 4
     ringLMod ringLMod      |
| 45 | 5, 10, 11, 19, 24, 29, 32, 35, 40, 44 | lsspropdg 14403 |
. . 3
        ringLMod ringLMod         ringLMod ringLMod     |
| 46 | | lidlvalg 14443 |
. . . 4
       LIdeal LIdeal        ringLMod ringLMod     |
| 47 | 2, 46 | syl 14 |
. . 3
     LIdeal LIdeal        ringLMod ringLMod     |
| 48 | | lidlvalg 14443 |
. . . 4
       LIdeal LIdeal        ringLMod ringLMod     |
| 49 | 7, 48 | syl 14 |
. . 3
     LIdeal LIdeal        ringLMod ringLMod     |
| 50 | 45, 47, 49 | 3eqtr4d 2272 |
. 2
     LIdeal LIdeal     LIdeal LIdeal    |
| 51 | 5, 10, 11, 19, 24, 29, 32, 35, 40, 44 | lsppropd 14404 |
. . 3
     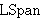   ringLMod ringLMod      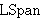   ringLMod ringLMod     |
| 52 | | rspvalg 14444 |
. . . 4
       RSpan RSpan     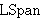   ringLMod ringLMod     |
| 53 | 2, 52 | syl 14 |
. . 3
     RSpan RSpan     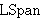   ringLMod ringLMod     |
| 54 | | rspvalg 14444 |
. . . 4
       RSpan RSpan     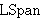   ringLMod ringLMod     |
| 55 | 7, 54 | syl 14 |
. . 3
     RSpan RSpan     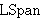   ringLMod ringLMod     |
| 56 | 51, 53, 55 | 3eqtr4d 2272 |
. 2
     RSpan RSpan     RSpan RSpan    |
| 57 | 50, 56 | jca 306 |
1
      LIdeal LIdeal     LIdeal LIdeal     RSpan RSpan     RSpan RSpan     |