Description: Define the value of an
operation. Definition of operation value in
[Enderton] p. 79. Note that the syntax
is simply three class expressions
in a row bracketed by parentheses. There are no restrictions of any kind
on what those class expressions may be, although only certain kinds of
class expressions - a binary operation  and its arguments  and
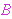 - will be useful
for proving meaningful theorems. For example, if
class is the
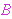operation + and arguments and are 3
and 2 ,
the expression ( 3 + 2 ) can be proved to equal 5 . This definition is
well-defined, although not very meaningful, when classes and/or
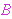are proper
classes (i.e. are not sets); see ovprc1 6065 and ovprc2 6066.
On the other hand, we often find uses for this definition when is a
proper class. is
normally equal to a class of nested ordered pairs
of the form defined by df-oprab 6032. (Contributed by NM,
28-Feb-1995.) |
