dedekindicclemicc - Intuitionistic Logic Explorer

	Intuitionistic Logic Explorer		< Previous Next > Nearby theorems
Mirrors > Home > ILE Home > Th. List > dedekindicclemicc		Unicode version

Theorem dedekindicclemicc 15104

Description: Lemma for dedekindicc 15105. Same as dedekindicc 15105, except that we merely show

to be an element of

. Later we will strengthen that to

. (Contributed by Jim Kingdon, 5-Jan-2024.)

**Hypotheses**
Ref	Expression
dedekindicc.a
dedekindicc.b
dedekindicc.lss
dedekindicc.uss
dedekindicc.lm
dedekindicc.um
dedekindicc.lr
dedekindicc.ur
dedekindicc.disj
dedekindicc.loc	$\/$
dedekindicc.ab

**Assertion**
Ref	Expression
dedekindicclemicc	$/\$

Distinct variable groups:

Proof of Theorem dedekindicclemicc Dummy variable

is distinct from all other variables.

Step	Hyp	Ref	Expression
1		dedekindicc.a	. . 3
2		dedekindicc.b	. . 3
3		dedekindicc.lss	. . 3
4		dedekindicc.uss	. . 3
5		dedekindicc.lm	. . 3
6		dedekindicc.um	. . 3
7		dedekindicc.lr	. . 3
8		dedekindicc.ur	. . 3
9		dedekindicc.disj	. . 3
10		dedekindicc.loc	. . 3 $\/$
11		dedekindicc.ab	. . 3
12	1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11	dedekindicclemlu 15102	. 2 $/\$
13	1	ad4antr 494	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
14	2	ad4antr 494	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
15	3	ad4antr 494	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
16	4	ad4antr 494	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
17	5	ad4antr 494	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
18	6	ad4antr 494	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
19	7	ad4antr 494	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
20	8	ad4antr 494	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
21	9	ad4antr 494	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
22	10	ad4antr 494	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$ $\/$
23	11	ad4antr 494	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
24		simprll 537	. . . . . . . . . . 11 $/\$ $/\$ $/\$ $/\$
25	24	ad3antrrr 492	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
26		simprr 531	. . . . . . . . . . 11 $/\$ $/\$ $/\$ $/\$ $/\$
27	26	ad3antrrr 492	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$ $/\$
28		simprlr 538	. . . . . . . . . . 11 $/\$ $/\$ $/\$ $/\$
29	28	ad3antrrr 492	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
30		simpllr 534	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$ $/\$
31		simpr 110	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
32	13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 25, 27, 29, 30, 31	dedekindicclemeu 15103	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
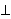33	1	ad4antr 494	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
34	2	ad4antr 494	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
35	3	ad4antr 494	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
36	4	ad4antr 494	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
37	5	ad4antr 494	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
38	6	ad4antr 494	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
39	7	ad4antr 494	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
40	8	ad4antr 494	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
41	9	ad4antr 494	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
42	10	ad4antr 494	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$ $\/$
43	11	ad4antr 494	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
44	28	ad3antrrr 492	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
45		simpllr 534	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$ $/\$
46	24	ad3antrrr 492	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
47	26	ad3antrrr 492	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$ $/\$
48		simpr 110	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
49	33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48	dedekindicclemeu 15103	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $/\$
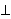50		simpr 110	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # #
51		iccssre 10077	. . . . . . . . . . . . . 14 $/\$
52	1, 2, 51	syl2anc 411	. . . . . . . . . . . . 13
53	52	ad3antrrr 492	. . . . . . . . . . . 12 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ #
54	24	ad2antrr 488	. . . . . . . . . . . 12 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ #
55	53, 54	sseldd 3194	. . . . . . . . . . 11 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ #
56	28	ad2antrr 488	. . . . . . . . . . . 12 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ #
57	53, 56	sseldd 3194	. . . . . . . . . . 11 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ #
58		reaplt 8661	. . . . . . . . . . 11 $/\$ # $\/$
59	55, 57, 58	syl2anc 411	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # # $\/$
60	50, 59	mpbid 147	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ # $\/$
61	32, 49, 60	mpjaodan 800	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ #
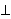62	61	inegd 1392	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ #
63	52	ad2antrr 488	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
64	24	adantr 276	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
65	63, 64	sseldd 3194	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
66	65	recnd 8101	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
67	28	adantr 276	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
68	63, 67	sseldd 3194	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
69	68	recnd 8101	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
70		apti 8695	. . . . . . . 8 $/\$ #
71	66, 69, 70	syl2anc 411	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ #
72	62, 71	mpbird 167	. . . . . 6 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
73		ancom 266	. . . . . . . . . . . . . . 15 $/\$ $/\$
74	73	anbi2i 457	. . . . . . . . . . . . . 14 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
75		anass 401	. . . . . . . . . . . . . 14 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
76	74, 75	bitr4i 187	. . . . . . . . . . . . 13 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
77	76	anbi2i 457	. . . . . . . . . . . 12 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
78		anass 401	. . . . . . . . . . . 12 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
79	77, 78	bitr4i 187	. . . . . . . . . . 11 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
80	79	anbi1i 458	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
81		anass 401	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
82	80, 81	bitri 184	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
83		anass 401	. . . . . . . . . . . 12 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
84	83	bicomi 132	. . . . . . . . . . 11 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
85	84	anbi1i 458	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
86		anass 401	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
87	85, 86	bitri 184	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
88	82, 87	bitri 184	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
89		anass 401	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
90		ancom 266	. . . . . . . . . . 11 $/\$ $/\$
91	90	anbi1i 458	. . . . . . . . . 10 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
92	89, 91	bitr3i 186	. . . . . . . . 9 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
93	92	anbi2i 457	. . . . . . . 8 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
94	88, 93	bitri 184	. . . . . . 7 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
95	94	imbi1i 238	. . . . . 6 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
96	72, 95	mpbi 145	. . . . 5 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
97	96	ex 115	. . . 4 $/\$ $/\$ $/\$ $/\$ $/\$
98	97	ralrimivva 2588	. . 3 $/\$ $/\$ $/\$
99		breq2 4048	. . . . . 6
100	99	ralbidv 2506	. . . . 5
101		breq1 4047	. . . . . 6
102	101	ralbidv 2506	. . . . 5
103	100, 102	anbi12d 473	. . . 4 $/\$ $/\$
104	103	rmo4 2966	. . 3 $/\$ $/\$ $/\$ $/\$
105	98, 104	sylibr 134	. 2 $/\$
106		reu5 2723	. 2 $/\$ $/\$ $/\$ $/\$
107	12, 105, 106	sylanbrc 417	1 $/\$

Colors of variables: wff set class

Syntax hints:

wn 3

wi 4 $/\$ wa 104

wb 105 $\/$ wo 710

wceq 1373

wfal 1378

wcel 2176

wral 2484

wrex 2485

wreu 2486

wrmo 2487

cin 3165

wss 3166

c0 3460 class class class wbr 4044 (class class class)co 5944

cc 7923

cr 7924

clt 8107 # cap 8654

cicc 10013

This theorem was proved from axioms: ax-mp 5 ax-1 6 ax-2 7 ax-ia1 106 ax-ia2 107 ax-ia3 108 ax-in1 615 ax-in2 616 ax-io 711 ax-5 1470 ax-7 1471 ax-gen 1472 ax-ie1 1516 ax-ie2 1517 ax-8 1527 ax-10 1528 ax-11 1529 ax-i12 1530 ax-bndl 1532 ax-4 1533 ax-17 1549 ax-i9 1553 ax-ial 1557 ax-i5r 1558 ax-13 2178 ax-14 2179 ax-ext 2187 ax-coll 4159 ax-sep 4162 ax-nul 4170 ax-pow 4218 ax-pr 4253 ax-un 4480 ax-setind 4585 ax-iinf 4636 ax-cnex 8016 ax-resscn 8017 ax-1cn 8018 ax-1re 8019 ax-icn 8020 ax-addcl 8021 ax-addrcl 8022 ax-mulcl 8023 ax-mulrcl 8024 ax-addcom 8025 ax-mulcom 8026 ax-addass 8027 ax-mulass 8028 ax-distr 8029 ax-i2m1 8030 ax-0lt1 8031 ax-1rid 8032 ax-0id 8033 ax-rnegex 8034 ax-precex 8035 ax-cnre 8036 ax-pre-ltirr 8037 ax-pre-ltwlin 8038 ax-pre-lttrn 8039 ax-pre-apti 8040 ax-pre-ltadd 8041 ax-pre-mulgt0 8042 ax-pre-mulext 8043 ax-arch 8044 ax-caucvg 8045 ax-pre-suploc 8046

This theorem depends on definitions: df-bi 117 df-dc 837 df-3or 982 df-3an 983 df-tru 1376 df-fal 1379 df-nf 1484 df-sb 1786 df-eu 2057 df-mo 2058 df-clab 2192 df-cleq 2198 df-clel 2201 df-nfc 2337 df-ne 2377 df-nel 2472 df-ral 2489 df-rex 2490 df-reu 2491 df-rmo 2492 df-rab 2493 df-v 2774 df-sbc 2999 df-csb 3094 df-dif 3168 df-un 3170 df-in 3172 df-ss 3179 df-nul 3461 df-if 3572 df-pw 3618 df-sn 3639 df-pr 3640 df-op 3642 df-uni 3851 df-int 3886 df-iun 3929 df-br 4045 df-opab 4106 df-mpt 4107 df-tr 4143 df-id 4340 df-po 4343 df-iso 4344 df-iord 4413 df-on 4415 df-ilim 4416 df-suc 4418 df-iom 4639 df-xp 4681 df-rel 4682 df-cnv 4683 df-co 4684 df-dm 4685 df-rn 4686 df-res 4687 df-ima 4688 df-iota 5232 df-fun 5273 df-fn 5274 df-f 5275 df-f1 5276 df-fo 5277 df-f1o 5278 df-fv 5279 df-isom 5280 df-riota 5899 df-ov 5947 df-oprab 5948 df-mpo 5949 df-1st 6226 df-2nd 6227 df-recs 6391 df-frec 6477 df-sup 7086 df-inf 7087 df-pnf 8109 df-mnf 8110 df-xr 8111 df-ltxr 8112 df-le 8113 df-sub 8245 df-neg 8246 df-reap 8648 df-ap 8655 df-div 8746 df-inn 9037 df-2 9095 df-3 9096 df-4 9097 df-n0 9296 df-z 9373 df-uz 9649 df-rp 9776 df-icc 10017 df-seqfrec 10593 df-exp 10684 df-cj 11153 df-re 11154 df-im 11155 df-rsqrt 11309 df-abs 11310

This theorem is referenced by: dedekindicc 15105

W3C validator