Theorem frecsuclem 6552

Description: Lemma for frecsuc 6553. Just giving a name to a common expression to simplify the proof. (Contributed by Jim Kingdon, 29-Mar-2022.)

Hypothesis

Ref	Expression
frecsuclem.g	|- G = ( g e. _V |-> { x | ( E. m e. om ( dom g = suc m /\ x e. ( F ` ( g ` m ) ) ) \/ ( dom g = (/) /\ x e. A ) ) } )

Assertion

Ref	Expression
frecsuclem	|- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> (frec ( F , A ) ` suc B ) = ( F ` (frec ( F , A ) ` B ) ) )

Distinct variable groups:   A, g, m, x   B, g, m, x   g, F, m, x   z, F, m, x   g, G, m, x   S, m, x, z

Allowed substitution hints:   A( z)   B( z)   S( g)   G( z)

Proof of Theorem frecsuclem

Dummy variables f w y are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		df-frec 6537	. . . . . . . . . . . . 13 |- frec ( F , A ) = (recs ( ( g e. _V |-> { x | ( E. m e. om ( dom g = suc m /\ x e. ( F ` ( g ` m ) ) ) \/ ( dom g = (/) /\ x e. A ) ) } ) ) |` om )
2		frecsuclem.g	. . . . . . . . . . . . . . 15 |- G = ( g e. _V |-> { x | ( E. m e. om ( dom g = suc m /\ x e. ( F ` ( g ` m ) ) ) \/ ( dom g = (/) /\ x e. A ) ) } )
3		recseq 6452	. . . . . . . . . . . . . . 15 |- ( G = ( g e. _V |-> { x | ( E. m e. om ( dom g = suc m /\ x e. ( F ` ( g ` m ) ) ) \/ ( dom g = (/) /\ x e. A ) ) } ) -> recs ( G ) = recs ( ( g e. _V |-> { x | ( E. m e. om ( dom g = suc m /\ x e. ( F ` ( g ` m ) ) ) \/ ( dom g = (/) /\ x e. A ) ) } ) ) )
4	2, 3	ax-mp 5	. . . . . . . . . . . . . 14 |- recs ( G ) = recs ( ( g e. _V |-> { x | ( E. m e. om ( dom g = suc m /\ x e. ( F ` ( g ` m ) ) ) \/ ( dom g = (/) /\ x e. A ) ) } ) )
5	4	reseq1i 5001	. . . . . . . . . . . . 13 |- (recs ( G ) |` om ) = (recs ( ( g e. _V |-> { x | ( E. m e. om ( dom g = suc m /\ x e. ( F ` ( g ` m ) ) ) \/ ( dom g = (/) /\ x e. A ) ) } ) ) |` om )
6	1, 5	eqtr4i 2253	. . . . . . . . . . . 12 |- frec ( F , A ) = (recs ( G ) |` om )
7	6	fveq1i 5628	. . . . . . . . . . 11 |- (frec ( F , A ) ` suc B ) = ( (recs ( G ) |` om ) ` suc B )
8		peano2 4687	. . . . . . . . . . . 12 |- ( B e. om -> suc B e. om )
9		fvres 5651	. . . . . . . . . . . 12 |- ( suc B e. om -> ( (recs ( G ) |` om ) ` suc B ) = (recs ( G ) ` suc B ) )
10	8, 9	syl 14	. . . . . . . . . . 11 |- ( B e. om -> ( (recs ( G ) |` om ) ` suc B ) = (recs ( G ) ` suc B ) )
11	7, 10	eqtrid 2274	. . . . . . . . . 10 |- ( B e. om -> (frec ( F , A ) ` suc B ) = (recs ( G ) ` suc B ) )
12	11	3ad2ant3 1044	. . . . . . . . 9 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> (frec ( F , A ) ` suc B ) = (recs ( G ) ` suc B ) )
13		eqid 2229	. . . . . . . . . . 11 |- recs ( G ) = recs ( G )
14	2	funmpt2 5357	. . . . . . . . . . . 12 |- Fun G
15	14	a1i 9	. . . . . . . . . . 11 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> Fun G )
16		ordom 4699	. . . . . . . . . . . 12 |- Ord om
17	16	a1i 9	. . . . . . . . . . 11 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> Ord om )
18		vex 2802	. . . . . . . . . . . . . 14 |- f e. _V
19	18	a1i 9	. . . . . . . . . . . . 13 |- ( ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) /\ y e. om /\ f : y --> S ) -> f e. _V )
20		simp2 1022	. . . . . . . . . . . . . 14 |- ( ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) /\ y e. om /\ f : y --> S ) -> y e. om )
21		simp3 1023	. . . . . . . . . . . . . 14 |- ( ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) /\ y e. om /\ f : y --> S ) -> f : y --> S )
22		simp11 1051	. . . . . . . . . . . . . . 15 |- ( ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) /\ y e. om /\ f : y --> S ) -> A. z e. S ( F ` z ) e. S )
23		fveq2 5627	. . . . . . . . . . . . . . . . 17 |- ( z = w -> ( F ` z ) = ( F ` w ) )
24	23	eleq1d 2298	. . . . . . . . . . . . . . . 16 |- ( z = w -> ( ( F ` z ) e. S <-> ( F ` w ) e. S ) )
25	24	cbvralv 2765	. . . . . . . . . . . . . . 15 |- ( A. z e. S ( F ` z ) e. S <-> A. w e. S ( F ` w ) e. S )
26	22, 25	sylib 122	. . . . . . . . . . . . . 14 |- ( ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) /\ y e. om /\ f : y --> S ) -> A. w e. S ( F ` w ) e. S )
27		simp12 1052	. . . . . . . . . . . . . 14 |- ( ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) /\ y e. om /\ f : y --> S ) -> A e. S )
28	20, 21, 26, 27	frecabcl 6545	. . . . . . . . . . . . 13 |- ( ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) /\ y e. om /\ f : y --> S ) -> { x | ( E. m e. om ( dom f = suc m /\ x e. ( F ` ( f ` m ) ) ) \/ ( dom f = (/) /\ x e. A ) ) } e. S )
29		dmeq 4923	. . . . . . . . . . . . . . . . . . 19 |- ( g = f -> dom g = dom f )
30	29	eqeq1d 2238	. . . . . . . . . . . . . . . . . 18 |- ( g = f -> ( dom g = suc m <-> dom f = suc m ) )
31		fveq1 5626	. . . . . . . . . . . . . . . . . . . 20 |- ( g = f -> ( g ` m ) = ( f ` m ) )
32	31	fveq2d 5631	. . . . . . . . . . . . . . . . . . 19 |- ( g = f -> ( F ` ( g ` m ) ) = ( F ` ( f ` m ) ) )
33	32	eleq2d 2299	. . . . . . . . . . . . . . . . . 18 |- ( g = f -> ( x e. ( F ` ( g ` m ) ) <-> x e. ( F ` ( f ` m ) ) ) )
34	30, 33	anbi12d 473	. . . . . . . . . . . . . . . . 17 |- ( g = f -> ( ( dom g = suc m /\ x e. ( F ` ( g ` m ) ) ) <-> ( dom f = suc m /\ x e. ( F ` ( f ` m ) ) ) ) )
35	34	rexbidv 2531	. . . . . . . . . . . . . . . 16 |- ( g = f -> ( E. m e. om ( dom g = suc m /\ x e. ( F ` ( g ` m ) ) ) <-> E. m e. om ( dom f = suc m /\ x e. ( F ` ( f ` m ) ) ) ) )
36	29	eqeq1d 2238	. . . . . . . . . . . . . . . . 17 |- ( g = f -> ( dom g = (/) <-> dom f = (/) ) )
37	36	anbi1d 465	. . . . . . . . . . . . . . . 16 |- ( g = f -> ( ( dom g = (/) /\ x e. A ) <-> ( dom f = (/) /\ x e. A ) ) )
38	35, 37	orbi12d 798	. . . . . . . . . . . . . . 15 |- ( g = f -> ( ( E. m e. om ( dom g = suc m /\ x e. ( F ` ( g ` m ) ) ) \/ ( dom g = (/) /\ x e. A ) ) <-> ( E. m e. om ( dom f = suc m /\ x e. ( F ` ( f ` m ) ) ) \/ ( dom f = (/) /\ x e. A ) ) ) )
39	38	abbidv 2347	. . . . . . . . . . . . . 14 |- ( g = f -> { x | ( E. m e. om ( dom g = suc m /\ x e. ( F ` ( g ` m ) ) ) \/ ( dom g = (/) /\ x e. A ) ) } = { x | ( E. m e. om ( dom f = suc m /\ x e. ( F ` ( f ` m ) ) ) \/ ( dom f = (/) /\ x e. A ) ) } )
40	39, 2	fvmptg 5710	. . . . . . . . . . . . 13 |- ( ( f e. _V /\ { x | ( E. m e. om ( dom f = suc m /\ x e. ( F ` ( f ` m ) ) ) \/ ( dom f = (/) /\ x e. A ) ) } e. S ) -> ( G ` f ) = { x | ( E. m e. om ( dom f = suc m /\ x e. ( F ` ( f ` m ) ) ) \/ ( dom f = (/) /\ x e. A ) ) } )
41	19, 28, 40	syl2anc 411	. . . . . . . . . . . 12 |- ( ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) /\ y e. om /\ f : y --> S ) -> ( G ` f ) = { x | ( E. m e. om ( dom f = suc m /\ x e. ( F ` ( f ` m ) ) ) \/ ( dom f = (/) /\ x e. A ) ) } )
42	41, 28	eqeltrd 2306	. . . . . . . . . . 11 |- ( ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) /\ y e. om /\ f : y --> S ) -> ( G ` f ) e. S )
43		limom 4706	. . . . . . . . . . . . . . 15 |- Lim om
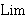44		limuni 4487	. . . . . . . . . . . . . . 15 |- ( Lim om -> om = U. om )
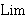
45	43, 44	ax-mp 5	. . . . . . . . . . . . . 14 |- om = U. om
46	45	eleq2i 2296	. . . . . . . . . . . . 13 |- ( y e. om <-> y e. U. om )
47		peano2 4687	. . . . . . . . . . . . 13 |- ( y e. om -> suc y e. om )
48	46, 47	sylbir 135	. . . . . . . . . . . 12 |- ( y e. U. om -> suc y e. om )
49	48	adantl 277	. . . . . . . . . . 11 |- ( ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) /\ y e. U. om ) -> suc y e. om )
50	45	eleq2i 2296	. . . . . . . . . . . . 13 |- ( suc B e. om <-> suc B e. U. om )
51	8, 50	sylib 122	. . . . . . . . . . . 12 |- ( B e. om -> suc B e. U. om )
52	51	3ad2ant3 1044	. . . . . . . . . . 11 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> suc B e. U. om )
53	13, 15, 17, 42, 49, 52	tfrcldm 6509	. . . . . . . . . 10 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> suc B e. dom recs ( G ) )
54	13	tfr2a 6467	. . . . . . . . . 10 |- ( suc B e. dom recs ( G ) -> (recs ( G ) ` suc B ) = ( G ` (recs ( G ) |` suc B ) ) )
55	53, 54	syl 14	. . . . . . . . 9 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> (recs ( G ) ` suc B ) = ( G ` (recs ( G ) |` suc B ) ) )
56	12, 55	eqtrd 2262	. . . . . . . 8 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> (frec ( F , A ) ` suc B ) = ( G ` (recs ( G ) |` suc B ) ) )
57		tfrfun 6466	. . . . . . . . . . 11 |- Fun recs ( G )
58	57	a1i 9	. . . . . . . . . 10 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> Fun recs ( G ) )
59	8	3ad2ant3 1044	. . . . . . . . . 10 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> suc B e. om )
60		resfunexg 5860	. . . . . . . . . 10 |- ( ( Fun recs ( G ) /\ suc B e. om ) -> (recs ( G ) |` suc B ) e. _V )
61	58, 59, 60	syl2anc 411	. . . . . . . . 9 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> (recs ( G ) |` suc B ) e. _V )
62		frecfcl 6551	. . . . . . . . . . . . 13 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S ) -> frec ( F , A ) : om --> S )
63	6	feq1i 5466	. . . . . . . . . . . . 13 |- (frec ( F , A ) : om --> S <-> (recs ( G ) |` om ) : om --> S )
64	62, 63	sylib 122	. . . . . . . . . . . 12 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S ) -> (recs ( G ) |` om ) : om --> S )
65	64	3adant3 1041	. . . . . . . . . . 11 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> (recs ( G ) |` om ) : om --> S )
66		simp3 1023	. . . . . . . . . . . 12 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> B e. om )
67		ordelsuc 4597	. . . . . . . . . . . . . 14 |- ( ( B e. om /\ Ord om ) -> ( B e. om <-> suc B C_ om ) )
68	16, 67	mpan2 425	. . . . . . . . . . . . 13 |- ( B e. om -> ( B e. om <-> suc B C_ om ) )
69	68	3ad2ant3 1044	. . . . . . . . . . . 12 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> ( B e. om <-> suc B C_ om ) )
70	66, 69	mpbid 147	. . . . . . . . . . 11 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> suc B C_ om )
71		fssres2 5503	. . . . . . . . . . 11 |- ( ( (recs ( G ) |` om ) : om --> S /\ suc B C_ om ) -> (recs ( G ) |` suc B ) : suc B --> S )
72	65, 70, 71	syl2anc 411	. . . . . . . . . 10 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> (recs ( G ) |` suc B ) : suc B --> S )
73		simp1 1021	. . . . . . . . . . 11 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> A. z e. S ( F ` z ) e. S )
74	73, 25	sylib 122	. . . . . . . . . 10 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> A. w e. S ( F ` w ) e. S )
75		simp2 1022	. . . . . . . . . 10 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> A e. S )
76	59, 72, 74, 75	frecabcl 6545	. . . . . . . . 9 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> { x | ( E. m e. om ( dom (recs ( G ) |` suc B ) = suc m /\ x e. ( F ` ( (recs ( G ) |` suc B ) ` m ) ) ) \/ ( dom (recs ( G ) |` suc B ) = (/) /\ x e. A ) ) } e. S )
77		dmeq 4923	. . . . . . . . . . . . . . 15 |- ( g = (recs ( G ) |` suc B ) -> dom g = dom (recs ( G ) |` suc B ) )
78	77	eqeq1d 2238	. . . . . . . . . . . . . 14 |- ( g = (recs ( G ) |` suc B ) -> ( dom g = suc m <-> dom (recs ( G ) |` suc B ) = suc m ) )
79		fveq1 5626	. . . . . . . . . . . . . . . 16 |- ( g = (recs ( G ) |` suc B ) -> ( g ` m ) = ( (recs ( G ) |` suc B ) ` m ) )
80	79	fveq2d 5631	. . . . . . . . . . . . . . 15 |- ( g = (recs ( G ) |` suc B ) -> ( F ` ( g ` m ) ) = ( F ` ( (recs ( G ) |` suc B ) ` m ) ) )
81	80	eleq2d 2299	. . . . . . . . . . . . . 14 |- ( g = (recs ( G ) |` suc B ) -> ( x e. ( F ` ( g ` m ) ) <-> x e. ( F ` ( (recs ( G ) |` suc B ) ` m ) ) ) )
82	78, 81	anbi12d 473	. . . . . . . . . . . . 13 |- ( g = (recs ( G ) |` suc B ) -> ( ( dom g = suc m /\ x e. ( F ` ( g ` m ) ) ) <-> ( dom (recs ( G ) |` suc B ) = suc m /\ x e. ( F ` ( (recs ( G ) |` suc B ) ` m ) ) ) ) )
83	82	rexbidv 2531	. . . . . . . . . . . 12 |- ( g = (recs ( G ) |` suc B ) -> ( E. m e. om ( dom g = suc m /\ x e. ( F ` ( g ` m ) ) ) <-> E. m e. om ( dom (recs ( G ) |` suc B ) = suc m /\ x e. ( F ` ( (recs ( G ) |` suc B ) ` m ) ) ) ) )
84	77	eqeq1d 2238	. . . . . . . . . . . . 13 |- ( g = (recs ( G ) |` suc B ) -> ( dom g = (/) <-> dom (recs ( G ) |` suc B ) = (/) ) )
85	84	anbi1d 465	. . . . . . . . . . . 12 |- ( g = (recs ( G ) |` suc B ) -> ( ( dom g = (/) /\ x e. A ) <-> ( dom (recs ( G ) |` suc B ) = (/) /\ x e. A ) ) )
86	83, 85	orbi12d 798	. . . . . . . . . . 11 |- ( g = (recs ( G ) |` suc B ) -> ( ( E. m e. om ( dom g = suc m /\ x e. ( F ` ( g ` m ) ) ) \/ ( dom g = (/) /\ x e. A ) ) <-> ( E. m e. om ( dom (recs ( G ) |` suc B ) = suc m /\ x e. ( F ` ( (recs ( G ) |` suc B ) ` m ) ) ) \/ ( dom (recs ( G ) |` suc B ) = (/) /\ x e. A ) ) ) )
87	86	abbidv 2347	. . . . . . . . . 10 |- ( g = (recs ( G ) |` suc B ) -> { x | ( E. m e. om ( dom g = suc m /\ x e. ( F ` ( g ` m ) ) ) \/ ( dom g = (/) /\ x e. A ) ) } = { x | ( E. m e. om ( dom (recs ( G ) |` suc B ) = suc m /\ x e. ( F ` ( (recs ( G ) |` suc B ) ` m ) ) ) \/ ( dom (recs ( G ) |` suc B ) = (/) /\ x e. A ) ) } )
88	87, 2	fvmptg 5710	. . . . . . . . 9 |- ( ( (recs ( G ) |` suc B ) e. _V /\ { x | ( E. m e. om ( dom (recs ( G ) |` suc B ) = suc m /\ x e. ( F ` ( (recs ( G ) |` suc B ) ` m ) ) ) \/ ( dom (recs ( G ) |` suc B ) = (/) /\ x e. A ) ) } e. S ) -> ( G ` (recs ( G ) |` suc B ) ) = { x | ( E. m e. om ( dom (recs ( G ) |` suc B ) = suc m /\ x e. ( F ` ( (recs ( G ) |` suc B ) ` m ) ) ) \/ ( dom (recs ( G ) |` suc B ) = (/) /\ x e. A ) ) } )
89	61, 76, 88	syl2anc 411	. . . . . . . 8 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> ( G ` (recs ( G ) |` suc B ) ) = { x | ( E. m e. om ( dom (recs ( G ) |` suc B ) = suc m /\ x e. ( F ` ( (recs ( G ) |` suc B ) ` m ) ) ) \/ ( dom (recs ( G ) |` suc B ) = (/) /\ x e. A ) ) } )
90	56, 89	eqtrd 2262	. . . . . . 7 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> (frec ( F , A ) ` suc B ) = { x | ( E. m e. om ( dom (recs ( G ) |` suc B ) = suc m /\ x e. ( F ` ( (recs ( G ) |` suc B ) ` m ) ) ) \/ ( dom (recs ( G ) |` suc B ) = (/) /\ x e. A ) ) } )
91	90	abeq2d 2342	. . . . . 6 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> ( x e. (frec ( F , A ) ` suc B ) <-> ( E. m e. om ( dom (recs ( G ) |` suc B ) = suc m /\ x e. ( F ` ( (recs ( G ) |` suc B ) ` m ) ) ) \/ ( dom (recs ( G ) |` suc B ) = (/) /\ x e. A ) ) ) )
92		fdm 5479	. . . . . . . . . . . 12 |- ( (recs ( G ) |` suc B ) : suc B --> S -> dom (recs ( G ) |` suc B ) = suc B )
93	72, 92	syl 14	. . . . . . . . . . 11 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> dom (recs ( G ) |` suc B ) = suc B )
94		peano3 4688	. . . . . . . . . . . 12 |- ( B e. om -> suc B =/= (/) )
95	94	3ad2ant3 1044	. . . . . . . . . . 11 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> suc B =/= (/) )
96	93, 95	eqnetrd 2424	. . . . . . . . . 10 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> dom (recs ( G ) |` suc B ) =/= (/) )
97	96	neneqd 2421	. . . . . . . . 9 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> -. dom (recs ( G ) |` suc B ) = (/) )
98	97	intnanrd 937	. . . . . . . 8 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> -. ( dom (recs ( G ) |` suc B ) = (/) /\ x e. A ) )
99		biorf 749	. . . . . . . 8 |- ( -. ( dom (recs ( G ) |` suc B ) = (/) /\ x e. A ) -> ( E. m e. om ( dom (recs ( G ) |` suc B ) = suc m /\ x e. ( F ` ( (recs ( G ) |` suc B ) ` m ) ) ) <-> ( ( dom (recs ( G ) |` suc B ) = (/) /\ x e. A ) \/ E. m e. om ( dom (recs ( G ) |` suc B ) = suc m /\ x e. ( F ` ( (recs ( G ) |` suc B ) ` m ) ) ) ) ) )
100	98, 99	syl 14	. . . . . . 7 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> ( E. m e. om ( dom (recs ( G ) |` suc B ) = suc m /\ x e. ( F ` ( (recs ( G ) |` suc B ) ` m ) ) ) <-> ( ( dom (recs ( G ) |` suc B ) = (/) /\ x e. A ) \/ E. m e. om ( dom (recs ( G ) |` suc B ) = suc m /\ x e. ( F ` ( (recs ( G ) |` suc B ) ` m ) ) ) ) ) )
101		orcom 733	. . . . . . 7 |- ( ( ( dom (recs ( G ) |` suc B ) = (/) /\ x e. A ) \/ E. m e. om ( dom (recs ( G ) |` suc B ) = suc m /\ x e. ( F ` ( (recs ( G ) |` suc B ) ` m ) ) ) ) <-> ( E. m e. om ( dom (recs ( G ) |` suc B ) = suc m /\ x e. ( F ` ( (recs ( G ) |` suc B ) ` m ) ) ) \/ ( dom (recs ( G ) |` suc B ) = (/) /\ x e. A ) ) )
102	100, 101	bitrdi 196	. . . . . 6 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> ( E. m e. om ( dom (recs ( G ) |` suc B ) = suc m /\ x e. ( F ` ( (recs ( G ) |` suc B ) ` m ) ) ) <-> ( E. m e. om ( dom (recs ( G ) |` suc B ) = suc m /\ x e. ( F ` ( (recs ( G ) |` suc B ) ` m ) ) ) \/ ( dom (recs ( G ) |` suc B ) = (/) /\ x e. A ) ) ) )
103	93	eqeq1d 2238	. . . . . . . . . 10 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> ( dom (recs ( G ) |` suc B ) = suc m <-> suc B = suc m ) )
104		vex 2802	. . . . . . . . . . . 12 |- m e. _V
105		suc11g 4649	. . . . . . . . . . . 12 |- ( ( B e. om /\ m e. _V ) -> ( suc B = suc m <-> B = m ) )
106	104, 105	mpan2 425	. . . . . . . . . . 11 |- ( B e. om -> ( suc B = suc m <-> B = m ) )
107	106	3ad2ant3 1044	. . . . . . . . . 10 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> ( suc B = suc m <-> B = m ) )
108	103, 107	bitrd 188	. . . . . . . . 9 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> ( dom (recs ( G ) |` suc B ) = suc m <-> B = m ) )
109		eqcom 2231	. . . . . . . . 9 |- ( B = m <-> m = B )
110	108, 109	bitrdi 196	. . . . . . . 8 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> ( dom (recs ( G ) |` suc B ) = suc m <-> m = B ) )
111	110	anbi1d 465	. . . . . . 7 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> ( ( dom (recs ( G ) |` suc B ) = suc m /\ x e. ( F ` ( (recs ( G ) |` suc B ) ` m ) ) ) <-> ( m = B /\ x e. ( F ` ( (recs ( G ) |` suc B ) ` m ) ) ) ) )
112	111	rexbidv 2531	. . . . . 6 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> ( E. m e. om ( dom (recs ( G ) |` suc B ) = suc m /\ x e. ( F ` ( (recs ( G ) |` suc B ) ` m ) ) ) <-> E. m e. om ( m = B /\ x e. ( F ` ( (recs ( G ) |` suc B ) ` m ) ) ) ) )
113	91, 102, 112	3bitr2d 216	. . . . 5 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> ( x e. (frec ( F , A ) ` suc B ) <-> E. m e. om ( m = B /\ x e. ( F ` ( (recs ( G ) |` suc B ) ` m ) ) ) ) )
114		fveq2 5627	. . . . . . . 8 |- ( m = B -> ( (recs ( G ) |` suc B ) ` m ) = ( (recs ( G ) |` suc B ) ` B ) )
115	114	fveq2d 5631	. . . . . . 7 |- ( m = B -> ( F ` ( (recs ( G ) |` suc B ) ` m ) ) = ( F ` ( (recs ( G ) |` suc B ) ` B ) ) )
116	115	eleq2d 2299	. . . . . 6 |- ( m = B -> ( x e. ( F ` ( (recs ( G ) |` suc B ) ` m ) ) <-> x e. ( F ` ( (recs ( G ) |` suc B ) ` B ) ) ) )
117	116	ceqsrexbv 2934	. . . . 5 |- ( E. m e. om ( m = B /\ x e. ( F ` ( (recs ( G ) |` suc B ) ` m ) ) ) <-> ( B e. om /\ x e. ( F ` ( (recs ( G ) |` suc B ) ` B ) ) ) )
118	113, 117	bitrdi 196	. . . 4 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> ( x e. (frec ( F , A ) ` suc B ) <-> ( B e. om /\ x e. ( F ` ( (recs ( G ) |` suc B ) ` B ) ) ) ) )
119	118	3anibar 1189	. . 3 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> ( x e. (frec ( F , A ) ` suc B ) <-> x e. ( F ` ( (recs ( G ) |` suc B ) ` B ) ) ) )
120	119	eqrdv 2227	. 2 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> (frec ( F , A ) ` suc B ) = ( F ` ( (recs ( G ) |` suc B ) ` B ) ) )
121		sucidg 4507	. . . . . 6 |- ( B e. om -> B e. suc B )
122		fvres 5651	. . . . . 6 |- ( B e. suc B -> ( (recs ( G ) |` suc B ) ` B ) = (recs ( G ) ` B ) )
123	121, 122	syl 14	. . . . 5 |- ( B e. om -> ( (recs ( G ) |` suc B ) ` B ) = (recs ( G ) ` B ) )
124	6	fveq1i 5628	. . . . . 6 |- (frec ( F , A ) ` B ) = ( (recs ( G ) |` om ) ` B )
125		fvres 5651	. . . . . 6 |- ( B e. om -> ( (recs ( G ) |` om ) ` B ) = (recs ( G ) ` B ) )
126	124, 125	eqtrid 2274	. . . . 5 |- ( B e. om -> (frec ( F , A ) ` B ) = (recs ( G ) ` B ) )
127	123, 126	eqtr4d 2265	. . . 4 |- ( B e. om -> ( (recs ( G ) |` suc B ) ` B ) = (frec ( F , A ) ` B ) )
128	127	3ad2ant3 1044	. . 3 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> ( (recs ( G ) |` suc B ) ` B ) = (frec ( F , A ) ` B ) )
129	128	fveq2d 5631	. 2 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> ( F ` ( (recs ( G ) |` suc B ) ` B ) ) = ( F ` (frec ( F , A ) ` B ) ) )
130	120, 129	eqtrd 2262	1 |- ( ( A. z e. S ( F ` z ) e. S /\ A e. S /\ B e. om ) -> (frec ( F , A ) ` suc B ) = ( F ` (frec ( F , A ) ` B ) ) )

Syntax hints:   -. wn 3   -> wi 4   /\ wa 104   <-> wb 105   \/ wo 713   /\ w3a 1002   = wceq 1395   e. wcel 2200   {cab 2215   =/= wne 2400   A.wral 2508   E.wrex 2509   _Vcvv 2799   C_ wss 3197   (/)c0 3491   U.cuni 3888   |-> cmpt 4145   Ord word 4453   Lim wlim 4455   suc csuc 4456   omcom 4682   dom cdm 4719   |` cres 4721   Fun wfun 5312   -->wf 5314   ` cfv 5318  recscrecs 6450  freccfrec 6536

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-ia1 106  ax-ia2 107  ax-ia3 108  ax-in1 617  ax-in2 618  ax-io 714  ax-5 1493  ax-7 1494  ax-gen 1495  ax-ie1 1539  ax-ie2 1540  ax-8 1550  ax-10 1551  ax-11 1552  ax-i12 1553  ax-bndl 1555  ax-4 1556  ax-17 1572  ax-i9 1576  ax-ial 1580  ax-i5r 1581  ax-13 2202  ax-14 2203  ax-ext 2211  ax-coll 4199  ax-sep 4202  ax-nul 4210  ax-pow 4258  ax-pr 4293  ax-un 4524  ax-setind 4629  ax-iinf 4680

This theorem depends on definitions:  df-bi 117  df-3an 1004  df-tru 1398  df-fal 1401  df-nf 1507  df-sb 1809  df-eu 2080  df-mo 2081  df-clab 2216  df-cleq 2222  df-clel 2225  df-nfc 2361  df-ne 2401  df-ral 2513  df-rex 2514  df-reu 2515  df-rab 2517  df-v 2801  df-sbc 3029  df-csb 3125  df-dif 3199  df-un 3201  df-in 3203  df-ss 3210  df-nul 3492  df-pw 3651  df-sn 3672  df-pr 3673  df-op 3675  df-uni 3889  df-int 3924  df-iun 3967  df-br 4084  df-opab 4146  df-mpt 4147  df-tr 4183  df-id 4384  df-iord 4457  df-on 4459  df-ilim 4460  df-suc 4462  df-iom 4683  df-xp 4725  df-rel 4726  df-cnv 4727  df-co 4728  df-dm 4729  df-rn 4730  df-res 4731  df-ima 4732  df-iota 5278  df-fun 5320  df-fn 5321  df-f 5322  df-f1 5323  df-fo 5324  df-f1o 5325  df-fv 5326  df-recs 6451  df-frec 6537

This theorem is referenced by:  frecsuc  6553