| Step | Hyp | Ref
| Expression |
|---|
| 1 | | caucvgprprlemaddq.ex |
. 2
         
     
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                   |
| 2 | | nfv 1574 |
. . 3
    |
| 3 | | nfcv 2372 |
. . . 4
    |
| 4 | | nfcv 2372 |
. . . 4
    |
| 5 | | caucvgprpr.lim |
. . . . . 6
               
               ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)               
                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)              
             |
| 6 | | nfre1 2573 |
. . . . . . . 8
         
               ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)              |
| 7 | | nfcv 2372 |
. . . . . . . 8
    |
| 8 | 6, 7 | nfrabw 2712 |
. . . . . . 7
              
               ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)               |
| 9 | | nfre1 2573 |
. . . . . . . 8
                             ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                          |
| 10 | 9, 7 | nfrabw 2712 |
. . . . . . 7
    
                             ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                           |
| 11 | 8, 10 | nfop 3873 |
. . . . . 6
               
               ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)               
                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)              
             |
| 12 | 5, 11 | nfcxfr 2369 |
. . . . 5
    |
| 13 | | nfcv 2372 |
. . . . 5
    |
| 14 | | nfcv 2372 |
. . . . 5
    |
| 15 | 12, 13, 14 | nfov 6037 |
. . . 4
        |
| 16 | 3, 4, 15 | nfbr 4130 |
. . 3
    
     |
| 17 | | caucvgprpr.f |
. . . . . . . . . . . 12
          |
| 18 | 17 | ad2antrr 488 |
. . . . . . . . . . 11
            
     
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                      
         |
| 19 | | caucvgprpr.cau |
. . . . . . . . . . . 12
                                              ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)                                     ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)           |
| 20 | 19 | ad2antrr 488 |
. . . . . . . . . . 11
            
     
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                      
                                             ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)                                     ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)           |
| 21 | | simpr 110 |
. . . . . . . . . . 11
            
     
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                      
       |
| 22 | | simplrl 535 |
. . . . . . . . . . 11
            
     
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                      
       |
| 23 | 18, 20, 21, 22 | caucvgprprlemnbj 7891 |
. . . . . . . . . 10
            
     
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                      
                 
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)               |
| 24 | 18, 21 | ffvelcdmd 5773 |
. . . . . . . . . . . . . 14
            
     
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                      
           |
| 25 | | recnnpr 7746 |
. . . . . . . . . . . . . . 15
                     ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)      
   |
| 26 | 25 | adantl 277 |
. . . . . . . . . . . . . 14
            
     
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                      
                  ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)          |
| 27 | | addclpr 7735 |
. . . . . . . . . . . . . 14
                          ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)                                 ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)           |
| 28 | 24, 26, 27 | syl2anc 411 |
. . . . . . . . . . . . 13
            
     
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                      
                         ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)           |
| 29 | | recnnpr 7746 |
. . . . . . . . . . . . . 14
                     ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)      
   |
| 30 | 22, 29 | syl 14 |
. . . . . . . . . . . . 13
            
     
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                      
                  ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)          |
| 31 | | caucvgprprlemaddq.q |
. . . . . . . . . . . . . 14
        |
| 32 | 31 | ad2antrr 488 |
. . . . . . . . . . . . 13
            
     
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                      
       |
| 33 | | addassprg 7777 |
. . . . . . . . . . . . 13
                         ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)                          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)      
                      
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)                                   ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)               
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)       
    |
| 34 | 28, 30, 32, 33 | syl3anc 1271 |
. . . . . . . . . . . 12
            
     
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                      
                 
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)                                   ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)               
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)       
    |
| 35 | 34 | breq1d 4093 |
. . . . . . . . . . 11
            
     
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                      
            
               ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)                  
                          ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)               
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)       
               |
| 36 | | ltaprg 7817 |
. . . . . . . . . . . . 13
        
           
        
    |
| 37 | 36 | adantl 277 |
. . . . . . . . . . . 12
                              ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                      
             
   
             
    |
| 38 | | addclpr 7735 |
. . . . . . . . . . . . 13
                         ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)                          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)      
                 
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)           |
| 39 | 28, 30, 38 | syl2anc 411 |
. . . . . . . . . . . 12
            
     
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                      
                          ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)              
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)           |
| 40 | 18, 22 | ffvelcdmd 5773 |
. . . . . . . . . . . 12
            
     
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                      
           |
| 41 | | addcomprg 7776 |
. . . . . . . . . . . . 13
        
               |
| 42 | 41 | adantl 277 |
. . . . . . . . . . . 12
                              ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                      
             
            |
| 43 | 37, 39, 40, 32, 42 | caovord2d 6181 |
. . . . . . . . . . 11
            
     
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                      
                 
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)                       
               ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)                  
    |
| 44 | | addcomprg 7776 |
. . . . . . . . . . . . . 14
                      ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)                             ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)                         ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)      
    |
| 45 | 32, 30, 44 | syl2anc 411 |
. . . . . . . . . . . . 13
            
     
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                      
                     ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)                         ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)      
    |
| 46 | 45 | oveq2d 6023 |
. . . . . . . . . . . 12
            
     
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                      
                          ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)                           ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)                 
               ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                         ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)            |
| 47 | 46 | breq1d 4093 |
. . . . . . . . . . 11
            
     
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                      
                 
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                 
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                                 
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                         ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)                  
    |
| 48 | 35, 43, 47 | 3bitr4rd 221 |
. . . . . . . . . 10
            
     
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                      
                 
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                 
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                                 
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)                |
| 49 | 23, 48 | mtbird 677 |
. . . . . . . . 9
            
     
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                      
                 
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                 
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                    |
| 50 | 49 | nrexdv 2623 |
. . . . . . . 8
    
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
                                 ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)                           ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)                    |
| 51 | | breq1 4086 |
. . . . . . . . . . . . . 14
                  ![] ]](rbrack.gif)   
           ![] ]](rbrack.gif)     |
| 52 | 51 | cbvabv 2354 |
. . . . . . . . . . . . 13
    
          ![] ]](rbrack.gif)    
   
          ![] ]](rbrack.gif)    |
| 53 | | breq2 4087 |
. . . . . . . . . . . . . 14
                ![] ]](rbrack.gif)               ![] ]](rbrack.gif)       |
| 54 | 53 | cbvabv 2354 |
. . . . . . . . . . . . 13
             ![] ]](rbrack.gif)                   ![] ]](rbrack.gif)      |
| 55 | 52, 54 | opeq12i 3862 |
. . . . . . . . . . . 12
     
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                       ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)       |
| 56 | 55 | oveq2i 6018 |
. . . . . . . . . . 11
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
               ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)        |
| 57 | | breq1 4086 |
. . . . . . . . . . . . . 14
                  ![] ]](rbrack.gif)   
           ![] ]](rbrack.gif)     |
| 58 | 57 | cbvabv 2354 |
. . . . . . . . . . . . 13
    
          ![] ]](rbrack.gif)    
   
          ![] ]](rbrack.gif)    |
| 59 | | breq2 4087 |
. . . . . . . . . . . . . 14
                ![] ]](rbrack.gif)               ![] ]](rbrack.gif)       |
| 60 | 59 | cbvabv 2354 |
. . . . . . . . . . . . 13
             ![] ]](rbrack.gif)                   ![] ]](rbrack.gif)      |
| 61 | 58, 60 | opeq12i 3862 |
. . . . . . . . . . . 12
     
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                       ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)       |
| 62 | 61 | oveq2i 6018 |
. . . . . . . . . . 11
         
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                           ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)        |
| 63 | 56, 62 | oveq12i 6019 |
. . . . . . . . . 10
        
    
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                           ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                 
               ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                 
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)         |
| 64 | 63 | breq1i 4090 |
. . . . . . . . 9
                         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                           ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                   
       
               ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                 
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                    |
| 65 | 64 | rexbii 2537 |
. . . . . . . 8
                             ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                           ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                   
                 
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                 
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                    |
| 66 | 50, 65 | sylnibr 681 |
. . . . . . 7
    
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
                                 ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                           ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                    |
| 67 | 17 | adantr 276 |
. . . . . . . 8
    
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
           |
| 68 | 19 | adantr 276 |
. . . . . . . 8
    
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
                                               ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)                                     ![] ]](rbrack.gif)      
          ![] ]](rbrack.gif)           |
| 69 | | caucvgprpr.bnd |
. . . . . . . . 9
                |
| 70 | 69 | adantr 276 |
. . . . . . . 8
    
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
                 |
| 71 | 31 | adantr 276 |
. . . . . . . 8
    
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
         |
| 72 | | simprl 529 |
. . . . . . . 8
    
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
         |
| 73 | 67, 68, 70, 5, 71, 72 | caucvgprprlemexb 7905 |
. . . . . . 7
    
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
                 
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                  
                 
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                 
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                     |
| 74 | 66, 73 | mtod 667 |
. . . . . 6
    
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
                 
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                   |
| 75 | | simprr 531 |
. . . . . . 7
    
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
   |
| 76 | | caucvgprprlemaddq.x |
. . . . . . . . . 10
        |
| 77 | 76 | adantr 276 |
. . . . . . . . 9
    
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
         |
| 78 | | recnnpr 7746 |
. . . . . . . . . 10
          
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)          |
| 79 | 72, 78 | syl 14 |
. . . . . . . . 9
    
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
         
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)          |
| 80 | | addclpr 7735 |
. . . . . . . . 9
         
            ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                   
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)           |
| 81 | 77, 79, 80 | syl2anc 411 |
. . . . . . . 8
    
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)           |
| 82 | 67, 72 | ffvelcdmd 5773 |
. . . . . . . . 9
    
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
             |
| 83 | | addclpr 7735 |
. . . . . . . . 9
            
               |
| 84 | 82, 71, 83 | syl2anc 411 |
. . . . . . . 8
    
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
           
     |
| 85 | 17, 19, 69, 5 | caucvgprprlemcl 7902 |
. . . . . . . . . . 11
        |
| 86 | 85 | adantr 276 |
. . . . . . . . . 10
    
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
         |
| 87 | | addclpr 7735 |
. . . . . . . . . 10
        
           |
| 88 | 86, 71, 87 | syl2anc 411 |
. . . . . . . . 9
    
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
             |
| 89 | | addclpr 7735 |
. . . . . . . . 9
             
            ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                 
    
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)           |
| 90 | 88, 79, 89 | syl2anc 411 |
. . . . . . . 8
    
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
           
    
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)           |
| 91 | | ltsopr 7794 |
. . . . . . . . 9
  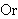  |
| 92 | | sowlin 4411 |
. . . . . . . . 9
    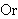                      ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                      
                      ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                      
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
         
            ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                    
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                    
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                     |
| 93 | 91, 92 | mpan 424 |
. . . . . . . 8
                     ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                      
                      ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                  
            ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                  
         
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
    
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                    
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                     |
| 94 | 81, 84, 90, 93 | syl3anc 1271 |
. . . . . . 7
    
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                  
         
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
    
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                    
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                     |
| 95 | 75, 94 | mpd 13 |
. . . . . 6
    
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                    
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                    
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                    |
| 96 | 74, 95 | ecased 1383 |
. . . . 5
    
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
    
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)         |
| 97 | 36 | adantl 277 |
. . . . . 6
            
     
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                               
   
             
    |
| 98 | 41 | adantl 277 |
. . . . . 6
            
     
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                               
            |
| 99 | 97, 77, 88, 79, 98 | caovord2d 6181 |
. . . . 5
    
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
                   
            ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                    
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)          |
| 100 | 96, 99 | mpbird 167 |
. . . 4
    
             
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)               
             |
| 101 | 100 | exp32 365 |
. . 3
               
            ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                  
          |
| 102 | 2, 16, 101 | rexlimd 2645 |
. 2
              
            ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                  
         |
| 103 | 1, 102 | mpd 13 |
1
     
      |