Proof of Theorem lgsdir2lem5
| Step | Hyp | Ref
| Expression |
|---|
| 1 | | 8nn 9289 |
. . . . . . . . 9
    |
| 2 | | zmodcl 10578 |
. . . . . . . . 9
        
           |
| 3 | 1, 2 | mpan2 425 |
. . . . . . . 8
              |
| 4 | 3 | adantr 276 |
. . . . . . 7
        
           |
| 5 | | elprg 3686 |
. . . . . . 7
        
             
                   |
| 6 | 4, 5 | syl 14 |
. . . . . 6
        
                                   |
| 7 | | zmodcl 10578 |
. . . . . . . . 9
        
           |
| 8 | 1, 7 | mpan2 425 |
. . . . . . . 8
              |
| 9 | 8 | adantl 277 |
. . . . . . 7
        
           |
| 10 | | elprg 3686 |
. . . . . . 7
        
             
                   |
| 11 | 9, 10 | syl 14 |
. . . . . 6
        
                                   |
| 12 | 6, 11 | anbi12d 473 |
. . . . 5
        
                             
                                       |
| 13 | | simpll 527 |
. . . . . . . . 9
                                 
  |
| 14 | | 3z 9486 |
. . . . . . . . . 10
    |
| 15 | 14 | a1i 9 |
. . . . . . . . 9
                                    |
| 16 | | simplr 528 |
. . . . . . . . 9
                                 
  |
| 17 | | nnq 9840 |
. . . . . . . . . . 11
          |
| 18 | 1, 17 | ax-mp 5 |
. . . . . . . . . 10
    |
| 19 | 18 | a1i 9 |
. . . . . . . . 9
                                    |
| 20 | | 8pos 9224 |
. . . . . . . . . 10
    |
| 21 | 20 | a1i 9 |
. . . . . . . . 9
                                 
  |
| 22 | | simprl 529 |
. . . . . . . . . 10
                                        |
| 23 | | lgsdir2lem1 15722 |
. . . . . . . . . . . 12
                                        |
| 24 | 23 | simpri 113 |
. . . . . . . . . . 11
                   |
| 25 | 24 | simpli 111 |
. . . . . . . . . 10
        |
| 26 | 22, 25 | eqtr4di 2280 |
. . . . . . . . 9
                                            |
| 27 | | simprr 531 |
. . . . . . . . . 10
                                        |
| 28 | 27, 25 | eqtr4di 2280 |
. . . . . . . . 9
                                            |
| 29 | 13, 15, 16, 15, 19, 21, 26, 28 | modqmul12d 10612 |
. . . . . . . 8
                                                    |
| 30 | 29 | orcd 738 |
. . . . . . 7
                                                                           |
| 31 | 30 | ex 115 |
. . . . . 6
        
                                                                  |
| 32 | | simpll 527 |
. . . . . . . . . 10
                                 
  |
| 33 | | znegcl 9488 |
. . . . . . . . . . 11
           |
| 34 | 14, 33 | mp1i 10 |
. . . . . . . . . 10
                                     |
| 35 | | simplr 528 |
. . . . . . . . . 10
                                 
  |
| 36 | 14 | a1i 9 |
. . . . . . . . . 10
                                    |
| 37 | 18 | a1i 9 |
. . . . . . . . . 10
                                    |
| 38 | 20 | a1i 9 |
. . . . . . . . . 10
                                 
  |
| 39 | | simprl 529 |
. . . . . . . . . . 11
                                        |
| 40 | 24 | simpri 113 |
. . . . . . . . . . 11
    
    |
| 41 | 39, 40 | eqtr4di 2280 |
. . . . . . . . . 10
                                         
   |
| 42 | | simprr 531 |
. . . . . . . . . . 11
                                        |
| 43 | 42, 25 | eqtr4di 2280 |
. . . . . . . . . 10
                                            |
| 44 | 32, 34, 35, 36, 37, 38, 41, 43 | modqmul12d 10612 |
. . . . . . . . 9
                                                     |
| 45 | | 3cn 9196 |
. . . . . . . . . . 11
    |
| 46 | 45, 45 | mulneg1i 8561 |
. . . . . . . . . 10
              |
| 47 | 46 | oveq1i 6017 |
. . . . . . . . 9
                      |
| 48 | 44, 47 | eqtrdi 2278 |
. . . . . . . 8
                                                     |
| 49 | 48 | olcd 739 |
. . . . . . 7
                                                                           |
| 50 | 49 | ex 115 |
. . . . . 6
        
                                                                  |
| 51 | | simpll 527 |
. . . . . . . . . 10
                                 
  |
| 52 | 14 | a1i 9 |
. . . . . . . . . 10
                                    |
| 53 | | simplr 528 |
. . . . . . . . . 10
                                 
  |
| 54 | 14, 33 | mp1i 10 |
. . . . . . . . . 10
                                     |
| 55 | 18 | a1i 9 |
. . . . . . . . . 10
                                    |
| 56 | 20 | a1i 9 |
. . . . . . . . . 10
                                 
  |
| 57 | | simprl 529 |
. . . . . . . . . . 11
                                        |
| 58 | 57, 25 | eqtr4di 2280 |
. . . . . . . . . 10
                                            |
| 59 | | simprr 531 |
. . . . . . . . . . 11
                                        |
| 60 | 59, 40 | eqtr4di 2280 |
. . . . . . . . . 10
                                         
   |
| 61 | 51, 52, 53, 54, 55, 56, 58, 60 | modqmul12d 10612 |
. . . . . . . . 9
                                                 
   |
| 62 | 45, 45 | mulneg2i 8562 |
. . . . . . . . . 10
              |
| 63 | 62 | oveq1i 6017 |
. . . . . . . . 9
        
             |
| 64 | 61, 63 | eqtrdi 2278 |
. . . . . . . 8
                                                     |
| 65 | 64 | olcd 739 |
. . . . . . 7
                                                                           |
| 66 | 65 | ex 115 |
. . . . . 6
        
                                                                  |
| 67 | | simpll 527 |
. . . . . . . . . 10
                                 
  |
| 68 | 14, 33 | mp1i 10 |
. . . . . . . . . 10
                                     |
| 69 | | simplr 528 |
. . . . . . . . . 10
                                 
  |
| 70 | 18 | a1i 9 |
. . . . . . . . . 10
                                    |
| 71 | 20 | a1i 9 |
. . . . . . . . . 10
                                 
  |
| 72 | | simprl 529 |
. . . . . . . . . . 11
                                        |
| 73 | 72, 40 | eqtr4di 2280 |
. . . . . . . . . 10
                                         
   |
| 74 | | simprr 531 |
. . . . . . . . . . 11
                                        |
| 75 | 74, 40 | eqtr4di 2280 |
. . . . . . . . . 10
                                         
   |
| 76 | 67, 68, 69, 68, 70, 71, 73, 75 | modqmul12d 10612 |
. . . . . . . . 9
                                                  
   |
| 77 | 45, 45 | mul2negi 8563 |
. . . . . . . . . 10
              |
| 78 | 77 | oveq1i 6017 |
. . . . . . . . 9
         
            |
| 79 | 76, 78 | eqtrdi 2278 |
. . . . . . . 8
                                                    |
| 80 | 79 | orcd 738 |
. . . . . . 7
                                                                           |
| 81 | 80 | ex 115 |
. . . . . 6
        
                                                                  |
| 82 | 31, 50, 66, 81 | ccased 971 |
. . . . 5
        
                                         
       
                   
                |
| 83 | 12, 82 | sylbid 150 |
. . . 4
        
                                                                          |
| 84 | 83 | imp 124 |
. . 3
                                                                                   |
| 85 | | simpll 527 |
. . . . . 6
                                         
  |
| 86 | | simplr 528 |
. . . . . 6
                                         
  |
| 87 | 85, 86 | zmulcld 9586 |
. . . . 5
                                                |
| 88 | 1 | a1i 9 |
. . . . 5
                                            |
| 89 | 87, 88 | zmodcld 10579 |
. . . 4
                                                    |
| 90 | | elprg 3686 |
. . . 4
        
   
        
                         
       
                   
                |
| 91 | 89, 90 | syl 14 |
. . 3
                                                                                                                      |
| 92 | 84, 91 | mpbird 167 |
. 2
                                                                         |
| 93 | | df-9 9187 |
. . . . . . . 8
 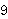       |
| 94 | | 8cn 9207 |
. . . . . . . . 9
    |
| 95 | | ax-1cn 8103 |
. . . . . . . . 9
    |
| 96 | 94, 95 | addcomi 8301 |
. . . . . . . 8
            |
| 97 | 93, 96 | eqtri 2250 |
. . . . . . 7
 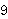       |
| 98 | | 3t3e9 9279 |
. . . . . . 7
       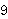 |
| 99 | 94 | mullidi 8160 |
. . . . . . . 8
        |
| 100 | 99 | oveq2i 6018 |
. . . . . . 7
                |
| 101 | 97, 98, 100 | 3eqtr4i 2260 |
. . . . . 6
                |
| 102 | 101 | oveq1i 6017 |
. . . . 5
                        |
| 103 | | 1nn 9132 |
. . . . . . 7
    |
| 104 | | nnq 9840 |
. . . . . . 7
          |
| 105 | 103, 104 | ax-mp 5 |
. . . . . 6
    |
| 106 | | 1z 9483 |
. . . . . 6
    |
| 107 | | modqcyc 10593 |
. . . . . 6
                                            |
| 108 | 105, 106,
18, 20, 107 | mp4an 427 |
. . . . 5
                    |
| 109 | 102, 108 | eqtri 2250 |
. . . 4
                |
| 110 | 23 | simpli 111 |
. . . . 5
                   |
| 111 | 110 | simpli 111 |
. . . 4
        |
| 112 | 109, 111 | eqtri 2250 |
. . 3
            |
| 113 | | znegcl 9488 |
. . . . . . . 8
           |
| 114 | 106, 113 | mp1i 10 |
. . . . . . 7
         |
| 115 | | 3nn 9284 |
. . . . . . . . . 10
    |
| 116 | 115, 115 | nnmulcli 9143 |
. . . . . . . . 9
        |
| 117 | 116 | nnzi 9478 |
. . . . . . . 8
        |
| 118 | 117 | a1i 9 |
. . . . . . 7
            |
| 119 | 106 | a1i 9 |
. . . . . . 7
    
   |
| 120 | 18 | a1i 9 |
. . . . . . 7
    
   |
| 121 | 20 | a1i 9 |
. . . . . . 7
    
   |
| 122 | | eqidd 2230 |
. . . . . . 7
                  |
| 123 | 109 | a1i 9 |
. . . . . . 7
                    |
| 124 | 114, 114,
118, 119, 120, 121, 122, 123 | modqmul12d 10612 |
. . . . . 6
                              |
| 125 | 124 | mptru 1404 |
. . . . 5
                          |
| 126 | 45, 45 | mulcli 8162 |
. . . . . . 7
        |
| 127 | 126 | mulm1i 8560 |
. . . . . 6
                  |
| 128 | 127 | oveq1i 6017 |
. . . . 5
                          |
| 129 | 95 | mulm1i 8560 |
. . . . . 6
          |
| 130 | 129 | oveq1i 6017 |
. . . . 5
                  |
| 131 | 125, 128,
130 | 3eqtr3i 2258 |
. . . 4
                  |
| 132 | 110 | simpri 113 |
. . . 4
    
    |
| 133 | 131, 132 | eqtri 2250 |
. . 3
             |
| 134 | 112, 133 | preq12i 3748 |
. 2
                             |
| 135 | 92, 134 | eleqtrdi 2322 |
1
                                                        |