| Step | Hyp | Ref
| Expression |
|---|
| 1 | | cdivcncf.1 |
. 2
            # #          |
| 2 | | simpl 109 |
. . . . 5
        
      # #         |
| 3 | | breq1 4086 |
. . . . . . . . 9
        # #  
 # #    |
| 4 | 3 | elrab 2959 |
. . . . . . . 8
          # #          # #    |
| 5 | 4 | biimpi 120 |
. . . . . . 7
          # #   
      # #    |
| 6 | 5 | adantl 277 |
. . . . . 6
        
      # #           # #    |
| 7 | 6 | simpld 112 |
. . . . 5
        
      # #         |
| 8 | 6 | simprd 114 |
. . . . 5
        
      # #      # #   |
| 9 | 2, 7, 8 | divrecapd 8951 |
. . . 4
        
      # #                     |
| 10 | 9 | mpteq2dva 4174 |
. . 3
               # #                    # #
              |
| 11 | | recclap 8837 |
. . . . . . 7
        # #            |
| 12 | 4, 11 | sylbi 121 |
. . . . . 6
          # #   
        |
| 13 | 12 | adantl 277 |
. . . . 5
        
      # #             |
| 14 | | oveq2 6015 |
. . . . . . 7
                  |
| 15 | 14 | cbvmptv 4180 |
. . . . . 6
          # #                    # #          |
| 16 | 15 | a1i 9 |
. . . . 5
               # #                    # #
          |
| 17 | | eqidd 2230 |
. . . . 5
                              |
| 18 | | oveq2 6015 |
. . . . 5
            
             |
| 19 | 13, 16, 17, 18 | fmptco 5803 |
. . . 4
             
              # #                     # #               |
| 20 | | breq1 4086 |
. . . . . . . . . 10
        # #  
 # #    |
| 21 | 20 | elrab 2959 |
. . . . . . . . 9
          # #          # #    |
| 22 | | recclap 8837 |
. . . . . . . . 9
        # #            |
| 23 | 21, 22 | sylbi 121 |
. . . . . . . 8
          # #   
        |
| 24 | 23 | adantl 277 |
. . . . . . 7
        
      # #             |
| 25 | 24 | fmpttd 5792 |
. . . . . 6
               # #                 # #      |
| 26 | | breq1 4086 |
. . . . . . . . 9
        # #  
 # #    |
| 27 | 26 | elrab 2959 |
. . . . . . . 8
          # #          # #    |
| 28 | | eqid 2229 |
. . . . . . . . . . . 12
  inf inf                                inf inf                              |
| 29 | 28 | reccn2ap 11840 |
. . . . . . . . . . 11
        # # 
                   # #
                                    |
| 30 | | eqidd 2230 |
. . . . . . . . . . . . . . . . . 18
          # #                     # #              # #
                   # #           |
| 31 | | oveq2 6015 |
. . . . . . . . . . . . . . . . . . 19
                  |
| 32 | 31 | adantl 277 |
. . . . . . . . . . . . . . . . . 18
           # #                     # #         
            |
| 33 | | simpr 110 |
. . . . . . . . . . . . . . . . . 18
          # #                     # #             # #    |
| 34 | | breq1 4086 |
. . . . . . . . . . . . . . . . . . . . 21
        # #  
 # #    |
| 35 | 34 | elrab 2959 |
. . . . . . . . . . . . . . . . . . . 20
          # #          # #    |
| 36 | | recclap 8837 |
. . . . . . . . . . . . . . . . . . . 20
        # #            |
| 37 | 35, 36 | sylbi 121 |
. . . . . . . . . . . . . . . . . . 19
          # #   
        |
| 38 | 37 | adantl 277 |
. . . . . . . . . . . . . . . . . 18
          # #                     # #             |
| 39 | 30, 32, 33, 38 | fvmptd 5717 |
. . . . . . . . . . . . . . . . 17
          # #                     # #               # #                    |
| 40 | | oveq2 6015 |
. . . . . . . . . . . . . . . . . . 19
                  |
| 41 | 40 | adantl 277 |
. . . . . . . . . . . . . . . . . 18
           # #                     # #         
            |
| 42 | | simpll1 1060 |
. . . . . . . . . . . . . . . . . . 19
          # #                     # #         |
| 43 | | simpll2 1061 |
. . . . . . . . . . . . . . . . . . 19
          # #                     # #      # #   |
| 44 | 26, 42, 43 | elrabd 2961 |
. . . . . . . . . . . . . . . . . 18
          # #                     # #             # #    |
| 45 | 42, 43 | recclapd 8939 |
. . . . . . . . . . . . . . . . . 18
          # #                     # #             |
| 46 | 30, 41, 44, 45 | fvmptd 5717 |
. . . . . . . . . . . . . . . . 17
          # #                     # #               # #                    |
| 47 | 39, 46 | oveq12d 6025 |
. . . . . . . . . . . . . . . 16
          # #                     # #                # #                        # #
                            |
| 48 | 47 | fveq2d 5633 |
. . . . . . . . . . . . . . 15
          # #                     # #                   # #
                       # #                                  |
| 49 | 48 | breq1d 4093 |
. . . . . . . . . . . . . 14
          # #                     # #                    # #                        # #                                       |
| 50 | 49 | imbi2d 230 |
. . . . . . . . . . . . 13
          # #                     # #                                 # #                        # #
                 
            
                      |
| 51 | 50 | ralbidva 2526 |
. . . . . . . . . . . 12
         # #               
       # #                              # #                        # #
                 
         # #
                                     |
| 52 | 51 | rexbidva 2527 |
. . . . . . . . . . 11
        # # 
        
           # #
                             # #
                       # #                    
           # #
                                     |
| 53 | 29, 52 | mpbird 167 |
. . . . . . . . . 10
        # # 
                   # #
                             # #
                       # #                   |
| 54 | 53 | 3expa 1227 |
. . . . . . . . 9
         # #     
    
           # #
                             # #
                       # #                   |
| 55 | 54 | ralrimiva 2603 |
. . . . . . . 8
        # #                     # #                              # #
                       # #                   |
| 56 | 27, 55 | sylbi 121 |
. . . . . . 7
          # #   
                 # #                              # #
                       # #                   |
| 57 | 56 | rgen 2583 |
. . . . . 6
          # #
   
               # #
                             # #
                       # #                  |
| 58 | | ssrab2 3309 |
. . . . . . 7
       # #     |
| 59 | | ssid 3244 |
. . . . . . 7
    |
| 60 | | elcncf2 15264 |
. . . . . . 7
         # #
        
           # #                  # #   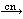              # #
                # #               # #                    # #                              # #
                       # #                     |
| 61 | 58, 59, 60 | mp2an 426 |
. . . . . 6
           # #                  # #   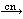              # #
                # #               # #                    # #                              # #
                       # #                    |
| 62 | 25, 57, 61 | sylanblrc 416 |
. . . . 5
               # #                  # #   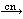    |
| 63 | | eqid 2229 |
. . . . . 6
                        |
| 64 | 63 | mulc1cncf 15279 |
. . . . 5
                    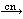    |
| 65 | 62, 64 | cncfco 15281 |
. . . 4
             
              # #                   # #   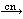    |
| 66 | 19, 65 | eqeltrrd 2307 |
. . 3
               # #                      # #   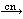    |
| 67 | 10, 66 | eqeltrd 2306 |
. 2
               # #                  # #   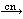    |
| 68 | 1, 67 | eqeltrid 2316 |
1
               # #   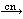    |