dvrecap - Intuitionistic Logic Explorer

	Intuitionistic Logic Explorer		< Previous Next > Nearby theorems
Mirrors > Home > ILE Home > Th. List > dvrecap		Unicode version

Theorem dvrecap 15524

Description: Derivative of the reciprocal function. (Contributed by Mario Carneiro, 25-Feb-2015.) (Revised by Mario Carneiro, 28-Dec-2016.)

**Assertion**
Ref	Expression
dvrecap	# #

Distinct variable group:

Proof of Theorem dvrecap Dummy variables

are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		funmpt 5371	. . . . . . . . 9 #
2		funforn 5575	. . . . . . . . 9 # # # #
3	1, 2	mpbi 145	. . . . . . . 8 # # #
4		fof 5568	. . . . . . . 8 # # # # # #
5	3, 4	ax-mp 5	. . . . . . 7 # # #
6		simpl 109	. . . . . . . . . 10 $/\$ #
7		breq1 4096	. . . . . . . . . . . . . 14 # #
8	7	elrab 2963	. . . . . . . . . . . . 13 # $/\$ #
9	8	biimpi 120	. . . . . . . . . . . 12 # $/\$ #
10	9	adantl 277	. . . . . . . . . . 11 $/\$ # $/\$ #
11	10	simpld 112	. . . . . . . . . 10 $/\$ #
12	10	simprd 114	. . . . . . . . . 10 $/\$ # #
13	6, 11, 12	divclapd 9029	. . . . . . . . 9 $/\$ #
14	13	ralrimiva 2606	. . . . . . . 8 #
15		eqid 2231	. . . . . . . . 9 # #
16	15	rnmptss 5816	. . . . . . . 8 # #
17	14, 16	syl 14	. . . . . . 7 #
18		fss 5501	. . . . . . 7 # # # $/\$ # # #
19	5, 17, 18	sylancr 414	. . . . . 6 # #
20	15	dmmpt 5239	. . . . . . 7 # #
21		ssrab2 3313	. . . . . . . 8 # #
22		ssrab2 3313	. . . . . . . 8 #
23	21, 22	sstri 3237	. . . . . . 7 #
24	20, 23	eqsstri 3260	. . . . . 6 #
25		cnex 8216	. . . . . . 7
26	25, 25	elpm2 6892	. . . . . 6 # # # $/\$ #
27	19, 24, 26	sylanblrc 416	. . . . 5 #
28		dvfcnpm 15501	. . . . 5 # # #
29	27, 28	syl 14	. . . 4 # #
30		ssidd 3249	. . . . . . 7
31		divclap 8917	. . . . . . . . . 10 $/\$ $/\$ #
32	31	3expb 1231	. . . . . . . . 9 $/\$ $/\$ #
33	8, 32	sylan2b 287	. . . . . . . 8 $/\$ #
34	33	fmpttd 5810	. . . . . . 7 # #
35	22	a1i 9	. . . . . . 7 #
36	30, 34, 35	dvbss 15496	. . . . . 6 # #
37		elrabi 2960	. . . . . . . 8 #
38	37	adantl 277	. . . . . . 7 $/\$ #
39		simpl 109	. . . . . . . . 9 $/\$ #
40	38	sqcld 10996	. . . . . . . . 9 $/\$ #
41		breq1 4096	. . . . . . . . . . . . 13 # #
42	41	elrab 2963	. . . . . . . . . . . 12 # $/\$ #
43	42	simprbi 275	. . . . . . . . . . 11 # #
44	43	adantl 277	. . . . . . . . . 10 $/\$ # #
45		sqap0 10931	. . . . . . . . . . 11 # #
46	38, 45	syl 14	. . . . . . . . . 10 $/\$ # # #
47	44, 46	mpbird 167	. . . . . . . . 9 $/\$ # #
48	39, 40, 47	divclapd 9029	. . . . . . . 8 $/\$ #
49	48	negcld 8536	. . . . . . 7 $/\$ #
50		simpr 110	. . . . . . . . 9 $/\$ # #
51		eqid 2231	. . . . . . . . . . 11
52	51	cntoptop 15344	. . . . . . . . . 10
53		0cn 8231	. . . . . . . . . . 11
54		cnopnap 15422	. . . . . . . . . . 11 #
55	53, 54	ax-mp 5	. . . . . . . . . 10 #
56		isopn3i 14946	. . . . . . . . . 10 $/\$ # # #
57	52, 55, 56	mp2an 426	. . . . . . . . 9 # #
58	50, 57	eleqtrrdi 2325	. . . . . . . 8 $/\$ # #
59	38	sqvald 10995	. . . . . . . . . . . . . 14 $/\$ #
60	59	oveq2d 6044	. . . . . . . . . . . . 13 $/\$ #
61	39, 38, 38, 44, 44	divdivap1d 9061	. . . . . . . . . . . . 13 $/\$ #
62	60, 61	eqtr4d 2267	. . . . . . . . . . . 12 $/\$ #
63	62	negeqd 8433	. . . . . . . . . . 11 $/\$ #
64	39, 38, 44	divclapd 9029	. . . . . . . . . . . 12 $/\$ #
65	64, 38, 44	divnegapd 9042	. . . . . . . . . . 11 $/\$ #
66	63, 65	eqtrd 2264	. . . . . . . . . 10 $/\$ #
67	64	negcld 8536	. . . . . . . . . . . 12 $/\$ #
68		eqid 2231	. . . . . . . . . . . . 13 # #
69	68	cdivcncfap 15415	. . . . . . . . . . . 12 # #
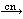70	67, 69	syl 14	. . . . . . . . . . 11 $/\$ # # #
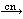71		oveq2 6036	. . . . . . . . . . 11
72	70, 50, 71	cnmptlimc 15485	. . . . . . . . . 10 $/\$ # # lim
73	66, 72	eqeltrd 2308	. . . . . . . . 9 $/\$ # # lim
74		cncff 15388	. . . . . . . . . . . 12 # # # #
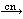75	70, 74	syl 14	. . . . . . . . . . 11 $/\$ # # #
76	22	a1i 9	. . . . . . . . . . 11 $/\$ # #
77	75, 76	limcdifap 15473	. . . . . . . . . 10 $/\$ # # lim # # # lim
78		elrabi 2960	. . . . . . . . . . . . . . . . . . . . 21 # # #
79	78	adantl 277	. . . . . . . . . . . . . . . . . . . 20 $/\$ # $/\$ # # #
80		breq1 4096	. . . . . . . . . . . . . . . . . . . . 21 # #
81	80	elrab 2963	. . . . . . . . . . . . . . . . . . . 20 # $/\$ #
82	79, 81	sylib 122	. . . . . . . . . . . . . . . . . . 19 $/\$ # $/\$ # # $/\$ #
83	82	simpld 112	. . . . . . . . . . . . . . . . . 18 $/\$ # $/\$ # #
84	37	ad2antlr 489	. . . . . . . . . . . . . . . . . 18 $/\$ # $/\$ # #
85	83, 84	subcld 8549	. . . . . . . . . . . . . . . . 17 $/\$ # $/\$ # #
86	64	adantr 276	. . . . . . . . . . . . . . . . . 18 $/\$ # $/\$ # #
87	81	simprbi 275	. . . . . . . . . . . . . . . . . . 19 # #
88	79, 87	syl 14	. . . . . . . . . . . . . . . . . 18 $/\$ # $/\$ # # #
89	86, 83, 88	divclapd 9029	. . . . . . . . . . . . . . . . 17 $/\$ # $/\$ # #
90		mulneg12 8635	. . . . . . . . . . . . . . . . 17 $/\$
91	85, 89, 90	syl2anc 411	. . . . . . . . . . . . . . . 16 $/\$ # $/\$ # #
92	84, 83, 89	subdird 8653	. . . . . . . . . . . . . . . . 17 $/\$ # $/\$ # #
93	83, 84	negsubdi2d 8565	. . . . . . . . . . . . . . . . . 18 $/\$ # $/\$ # #
94	93	oveq1d 6043	. . . . . . . . . . . . . . . . 17 $/\$ # $/\$ # #
95		oveq2 6036	. . . . . . . . . . . . . . . . . . . 20
96		simpll 527	. . . . . . . . . . . . . . . . . . . . 21 $/\$ # $/\$ # #
97	96, 83, 88	divclapd 9029	. . . . . . . . . . . . . . . . . . . 20 $/\$ # $/\$ # #
98	15, 95, 79, 97	fvmptd3 5749	. . . . . . . . . . . . . . . . . . 19 $/\$ # $/\$ # # #
99	43	ad2antlr 489	. . . . . . . . . . . . . . . . . . . . 21 $/\$ # $/\$ # # #
100	96, 84, 99	divcanap2d 9031	. . . . . . . . . . . . . . . . . . . 20 $/\$ # $/\$ # #
101	100	oveq1d 6043	. . . . . . . . . . . . . . . . . . 19 $/\$ # $/\$ # #
102	84, 86, 83, 88	divassapd 9065	. . . . . . . . . . . . . . . . . . 19 $/\$ # $/\$ # #
103	98, 101, 102	3eqtr2d 2270	. . . . . . . . . . . . . . . . . 18 $/\$ # $/\$ # # #
104		oveq2 6036	. . . . . . . . . . . . . . . . . . . 20
105	50	adantr 276	. . . . . . . . . . . . . . . . . . . 20 $/\$ # $/\$ # # #
106	15, 104, 105, 86	fvmptd3 5749	. . . . . . . . . . . . . . . . . . 19 $/\$ # $/\$ # # #
107	86, 83, 88	divcanap2d 9031	. . . . . . . . . . . . . . . . . . 19 $/\$ # $/\$ # #
108	106, 107	eqtr4d 2267	. . . . . . . . . . . . . . . . . 18 $/\$ # $/\$ # # #
109	103, 108	oveq12d 6046	. . . . . . . . . . . . . . . . 17 $/\$ # $/\$ # # # #
110	92, 94, 109	3eqtr4d 2274	. . . . . . . . . . . . . . . 16 $/\$ # $/\$ # # # #
111	86, 83, 88	divnegapd 9042	. . . . . . . . . . . . . . . . 17 $/\$ # $/\$ # #
112	111	oveq2d 6044	. . . . . . . . . . . . . . . 16 $/\$ # $/\$ # #
113	91, 110, 112	3eqtr3d 2272	. . . . . . . . . . . . . . 15 $/\$ # $/\$ # # # #
114	113	oveq1d 6043	. . . . . . . . . . . . . 14 $/\$ # $/\$ # # # #
115	86	negcld 8536	. . . . . . . . . . . . . . . 16 $/\$ # $/\$ # #
116	115, 83, 88	divclapd 9029	. . . . . . . . . . . . . . 15 $/\$ # $/\$ # #
117		breq1 4096	. . . . . . . . . . . . . . . . . . 19 # #
118	117	elrab 2963	. . . . . . . . . . . . . . . . . 18 # # # $/\$ #
119	118	simprbi 275	. . . . . . . . . . . . . . . . 17 # # #
120	119	adantl 277	. . . . . . . . . . . . . . . 16 $/\$ # $/\$ # # #
121	83, 84, 120	subap0d 8883	. . . . . . . . . . . . . . 15 $/\$ # $/\$ # # #
122	116, 85, 121	divcanap3d 9034	. . . . . . . . . . . . . 14 $/\$ # $/\$ # #
123	114, 122	eqtrd 2264	. . . . . . . . . . . . 13 $/\$ # $/\$ # # # #
124	123	mpteq2dva 4184	. . . . . . . . . . . 12 $/\$ # # # # # # #
125		ssrab2 3313	. . . . . . . . . . . . 13 # # #
126		resmpt 5067	. . . . . . . . . . . . 13 # # # # # # # #
127	125, 126	ax-mp 5	. . . . . . . . . . . 12 # # # # #
128	124, 127	eqtr4di 2282	. . . . . . . . . . 11 $/\$ # # # # # # # #
129	128	oveq1d 6043	. . . . . . . . . 10 $/\$ # # # # # lim # # # lim
130	77, 129	eqtr4d 2267	. . . . . . . . 9 $/\$ # # lim # # # # lim
131	73, 130	eleqtrd 2310	. . . . . . . 8 $/\$ # # # # # lim
132	51	cntoptopon 15343	. . . . . . . . . 10 TopOn
133	132	toponrestid 14832	. . . . . . . . 9 ↾_t
134		eqid 2231	. . . . . . . . 9 # # # # # # # #
135		ssidd 3249	. . . . . . . . 9 $/\$ #
136	34	adantr 276	. . . . . . . . 9 $/\$ # # #
137	133, 51, 134, 135, 136, 76	eldvap 15493	. . . . . . . 8 $/\$ # # # $/\$ # # # # lim
138	58, 131, 137	mpbir2and 953	. . . . . . 7 $/\$ # #
139		breldmg 4943	. . . . . . 7 $/\$ $/\$ # #
140	38, 49, 138, 139	syl3anc 1274	. . . . . 6 $/\$ # #
141	36, 140	eqelssd 3247	. . . . 5 # #
142	141	feq2d 5477	. . . 4 # # # #
143	29, 142	mpbid 147	. . 3 # #
144	143	ffnd 5490	. 2 # #
145	11	sqcld 10996	. . . . . 6 $/\$ #
146		sqap0 10931	. . . . . . . 8 # #
147	11, 146	syl 14	. . . . . . 7 $/\$ # # #
148	12, 147	mpbird 167	. . . . . 6 $/\$ # #
149	6, 145, 148	divclapd 9029	. . . . 5 $/\$ #
150	149	negcld 8536	. . . 4 $/\$ #
151	150	ralrimiva 2606	. . 3 #
152		eqid 2231	. . . 4 # #
153	152	fnmpt 5466	. . 3 # # #
154	151, 153	syl 14	. 2 # #
155	29	ffund 5493	. . . . 5 #
156	155	adantr 276	. . . 4 $/\$ # #
157		funbrfv 5691	. . . 4 # # #
158	156, 138, 157	sylc 62	. . 3 $/\$ # #
159		oveq1 6035	. . . . . 6
160	159	oveq2d 6044	. . . . 5
161	160	negeqd 8433	. . . 4
162	152, 161, 50, 49	fvmptd3 5749	. . 3 $/\$ # #
163	158, 162	eqtr4d 2267	. 2 $/\$ # # #
164	144, 154, 163	eqfnfvd 5756	1 # #

Colors of variables: wff set class

Syntax hints:

wi 4 $/\$ wa 104

wb 105

wceq 1398

wcel 2202

wral 2511

crab 2515

cvv 2803

wss 3201 class class class wbr 4093

cmpt 4155

cdm 4731

crn 4732

cres 4733

ccom 4735

wfun 5327

wfn 5328

wf 5329

wfo 5331

cfv 5333 (class class class)co 6028

cpm 6861

cc 8090

cc0 8092

cmul 8097

cmin 8409

cneg 8410 # cap 8820

cdiv 8911

c2 9253

cexp 10863

cabs 11637

cmopn 14637

ctop 14808

cnt 14904

ccncf 15381 lim

climc 15465

cdv 15466

This theorem was proved from axioms: ax-mp 5 ax-1 6 ax-2 7 ax-ia1 106 ax-ia2 107 ax-ia3 108 ax-in1 619 ax-in2 620 ax-io 717 ax-5 1496 ax-7 1497 ax-gen 1498 ax-ie1 1542 ax-ie2 1543 ax-8 1553 ax-10 1554 ax-11 1555 ax-i12 1556 ax-bndl 1558 ax-4 1559 ax-17 1575 ax-i9 1579 ax-ial 1583 ax-i5r 1584 ax-13 2204 ax-14 2205 ax-ext 2213 ax-coll 4209 ax-sep 4212 ax-nul 4220 ax-pow 4270 ax-pr 4305 ax-un 4536 ax-setind 4641 ax-iinf 4692 ax-cnex 8183 ax-resscn 8184 ax-1cn 8185 ax-1re 8186 ax-icn 8187 ax-addcl 8188 ax-addrcl 8189 ax-mulcl 8190 ax-mulrcl 8191 ax-addcom 8192 ax-mulcom 8193 ax-addass 8194 ax-mulass 8195 ax-distr 8196 ax-i2m1 8197 ax-0lt1 8198 ax-1rid 8199 ax-0id 8200 ax-rnegex 8201 ax-precex 8202 ax-cnre 8203 ax-pre-ltirr 8204 ax-pre-ltwlin 8205 ax-pre-lttrn 8206 ax-pre-apti 8207 ax-pre-ltadd 8208 ax-pre-mulgt0 8209 ax-pre-mulext 8210 ax-arch 8211 ax-caucvg 8212

This theorem depends on definitions: df-bi 117 df-stab 839 df-dc 843 df-3or 1006 df-3an 1007 df-tru 1401 df-fal 1404 df-nf 1510 df-sb 1811 df-eu 2082 df-mo 2083 df-clab 2218 df-cleq 2224 df-clel 2227 df-nfc 2364 df-ne 2404 df-nel 2499 df-ral 2516 df-rex 2517 df-reu 2518 df-rmo 2519 df-rab 2520 df-v 2805 df-sbc 3033 df-csb 3129 df-dif 3203 df-un 3205 df-in 3207 df-ss 3214 df-nul 3497 df-if 3608 df-pw 3658 df-sn 3679 df-pr 3680 df-op 3682 df-uni 3899 df-int 3934 df-iun 3977 df-br 4094 df-opab 4156 df-mpt 4157 df-tr 4193 df-id 4396 df-po 4399 df-iso 4400 df-iord 4469 df-on 4471 df-ilim 4472 df-suc 4474 df-iom 4695 df-xp 4737 df-rel 4738 df-cnv 4739 df-co 4740 df-dm 4741 df-rn 4742 df-res 4743 df-ima 4744 df-iota 5293 df-fun 5335 df-fn 5336 df-f 5337 df-f1 5338 df-fo 5339 df-f1o 5340 df-fv 5341 df-isom 5342 df-riota 5981 df-ov 6031 df-oprab 6032 df-mpo 6033 df-1st 6312 df-2nd 6313 df-recs 6514 df-frec 6600 df-map 6862 df-pm 6863 df-sup 7243 df-inf 7244 df-pnf 8275 df-mnf 8276 df-xr 8277 df-ltxr 8278 df-le 8279 df-sub 8411 df-neg 8412 df-reap 8814 df-ap 8821 df-div 8912 df-inn 9203 df-2 9261 df-3 9262 df-4 9263 df-n0 9462 df-z 9541 df-uz 9817 df-q 9915 df-rp 9950 df-xneg 10068 df-xadd 10069 df-seqfrec 10773 df-exp 10864 df-cj 11482 df-re 11483 df-im 11484 df-rsqrt 11638 df-abs 11639 df-rest 13404 df-topgen 13423 df-psmet 14639 df-xmet 14640 df-met 14641 df-bl 14642 df-mopn 14643 df-top 14809 df-topon 14822 df-bases 14854 df-ntr 14907 df-cn 14999 df-cnp 15000 df-cncf 15382 df-limced 15467 df-dvap 15468

This theorem is referenced by: (None)

W3C validator