ILE Home Intuitionistic Logic Explorer < Previous   Next >
Nearby theorems
Mirrors  >  Home  >  ILE Home  >  Th. List  >  suplocsrlem Unicode version
Theorem suplocsrlem 7875
Description: Lemma for suplocsr 7876. The set A has a least upper bound. (Contributed by Jim Kingdon, 16-Jan-2024.)
Hypotheses
Ref Expression
suplocsrlem.b |- B = { w e. P. | ( C +R [ <. w , 1P >. ] ~R ) e. A }
suplocsrlem.ss |- ( ph -> A C_ R. )
suplocsrlem.c |- ( ph -> C e. A )
suplocsrlem.ub |- ( ph -> E. x e. R. A. y e. A y <R x )
suplocsrlem.loc |- ( ph -> A. x e. R. A. y e. R. ( x <R y -> ( E. z e. A x <R z \/ A. z e. A z <R y ) ) )
Assertion
Ref Expression
suplocsrlem |- ( ph -> E. x e. R. ( A. y e. A -. x <R y /\ A. y e. R. ( y <R x -> E. z e. A y <R z ) ) )
Distinct variable groups:   w, A, x, y, z   w, B, y, z, x   w, C, y, z, x   ph, w, y, x, z
Proof of Theorem suplocsrlem
Dummy variables b u v a are mutually distinct and distinct from all other variables.
StepHypRef Expression
1 suplocsrlem.b . . 3 |- B = { w e. P. | ( C +R [ <. w , 1P >. ] ~R ) e. A }
2 suplocsrlem.ss . . 3 |- ( ph -> A C_ R. )
3 suplocsrlem.c . . 3 |- ( ph -> C e. A )
4 suplocsrlem.ub . . 3 |- ( ph -> E. x e. R. A. y e. A y <R x )
5 suplocsrlem.loc . . 3 |- ( ph -> A. x e. R. A. y e. R. ( x <R y -> ( E. z e. A x <R z \/ A. z e. A z <R y ) ) )
61, 2, 3, 4, 5suplocsrlempr 7874 . 2 |- ( ph -> E. v e. P. ( A. w e. B -. v <P w /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) )
7 simpr 110 . . . . . . 7 |- ( ( ph /\ v e. P. ) -> v e. P. )
82, 3sseldd 3184 . . . . . . . 8 |- ( ph -> C e. R. )
98adantr 276 . . . . . . 7 |- ( ( ph /\ v e. P. ) -> C e. R. )
10 mappsrprg 7871 . . . . . . 7 |- ( ( v e. P. /\ C e. R. ) -> ( C +R -1R ) <R ( C +R [ <. v , 1P >. ] ~R ) )
117, 9, 10syl2anc 411 . . . . . 6 |- ( ( ph /\ v e. P. ) -> ( C +R -1R ) <R ( C +R [ <. v , 1P >. ] ~R ) )
12 ltrelsr 7805 . . . . . . 7 |- <R C_ ( R. X. R. )
1312brel 4715 . . . . . 6 |- ( ( C +R -1R ) <R ( C +R [ <. v , 1P >. ] ~R ) -> ( ( C +R -1R ) e. R. /\ ( C +R [ <. v , 1P >. ] ~R ) e. R. ) )
1411, 13syl 14 . . . . 5 |- ( ( ph /\ v e. P. ) -> ( ( C +R -1R ) e. R. /\ ( C +R [ <. v , 1P >. ] ~R ) e. R. ) )
1514simprd 114 . . . 4 |- ( ( ph /\ v e. P. ) -> ( C +R [ <. v , 1P >. ] ~R ) e. R. )
16 breq2 4037 . . . . . . . 8 |- ( w = a -> ( v <P w <-> v <P a ) )
1716notbid 668 . . . . . . 7 |- ( w = a -> ( -. v <P w <-> -. v <P a ) )
1817cbvralv 2729 . . . . . 6 |- ( A. w e. B -. v <P w <-> A. a e. B -. v <P a )
19 ltsosr 7831 . . . . . . . . . . . . . . 15 |- <R Or R.
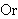2019, 12sotri 5065 . . . . . . . . . . . . . 14 |- ( ( ( C +R -1R ) <R ( C +R [ <. v , 1P >. ] ~R ) /\ ( C +R [ <. v , 1P >. ] ~R ) <R y ) -> ( C +R -1R ) <R y )
2111, 20sylan 283 . . . . . . . . . . . . 13 |- ( ( ( ph /\ v e. P. ) /\ ( C +R [ <. v , 1P >. ] ~R ) <R y ) -> ( C +R -1R ) <R y )
229adantr 276 . . . . . . . . . . . . . 14 |- ( ( ( ph /\ v e. P. ) /\ ( C +R [ <. v , 1P >. ] ~R ) <R y ) -> C e. R. )
23 map2psrprg 7872 . . . . . . . . . . . . . 14 |- ( C e. R. -> ( ( C +R -1R ) <R y <-> E. w e. P. ( C +R [ <. w , 1P >. ] ~R ) = y ) )
2422, 23syl 14 . . . . . . . . . . . . 13 |- ( ( ( ph /\ v e. P. ) /\ ( C +R [ <. v , 1P >. ] ~R ) <R y ) -> ( ( C +R -1R ) <R y <-> E. w e. P. ( C +R [ <. w , 1P >. ] ~R ) = y ) )
2521, 24mpbid 147 . . . . . . . . . . . 12 |- ( ( ( ph /\ v e. P. ) /\ ( C +R [ <. v , 1P >. ] ~R ) <R y ) -> E. w e. P. ( C +R [ <. w , 1P >. ] ~R ) = y )
2625adantlr 477 . . . . . . . . . . 11 |- ( ( ( ( ph /\ v e. P. ) /\ A. a e. B -. v <P a ) /\ ( C +R [ <. v , 1P >. ] ~R ) <R y ) -> E. w e. P. ( C +R [ <. w , 1P >. ] ~R ) = y )
2726adantlr 477 . . . . . . . . . 10 |- ( ( ( ( ( ph /\ v e. P. ) /\ A. a e. B -. v <P a ) /\ y e. A ) /\ ( C +R [ <. v , 1P >. ] ~R ) <R y ) -> E. w e. P. ( C +R [ <. w , 1P >. ] ~R ) = y )
28 simplr 528 . . . . . . . . . . . . 13 |- ( ( ( ( ( ( ph /\ v e. P. ) /\ A. a e. B -. v <P a ) /\ y e. A ) /\ ( C +R [ <. v , 1P >. ] ~R ) <R y ) /\ ( w e. P. /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) ) -> ( C +R [ <. v , 1P >. ] ~R ) <R y )
29 simprr 531 . . . . . . . . . . . . 13 |- ( ( ( ( ( ( ph /\ v e. P. ) /\ A. a e. B -. v <P a ) /\ y e. A ) /\ ( C +R [ <. v , 1P >. ] ~R ) <R y ) /\ ( w e. P. /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) ) -> ( C +R [ <. w , 1P >. ] ~R ) = y )
3028, 29breqtrrd 4061 . . . . . . . . . . . 12 |- ( ( ( ( ( ( ph /\ v e. P. ) /\ A. a e. B -. v <P a ) /\ y e. A ) /\ ( C +R [ <. v , 1P >. ] ~R ) <R y ) /\ ( w e. P. /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) ) -> ( C +R [ <. v , 1P >. ] ~R ) <R ( C +R [ <. w , 1P >. ] ~R ) )
317ad4antr 494 . . . . . . . . . . . . 13 |- ( ( ( ( ( ( ph /\ v e. P. ) /\ A. a e. B -. v <P a ) /\ y e. A ) /\ ( C +R [ <. v , 1P >. ] ~R ) <R y ) /\ ( w e. P. /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) ) -> v e. P. )
32 simprl 529 . . . . . . . . . . . . 13 |- ( ( ( ( ( ( ph /\ v e. P. ) /\ A. a e. B -. v <P a ) /\ y e. A ) /\ ( C +R [ <. v , 1P >. ] ~R ) <R y ) /\ ( w e. P. /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) ) -> w e. P. )
339ad4antr 494 . . . . . . . . . . . . 13 |- ( ( ( ( ( ( ph /\ v e. P. ) /\ A. a e. B -. v <P a ) /\ y e. A ) /\ ( C +R [ <. v , 1P >. ] ~R ) <R y ) /\ ( w e. P. /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) ) -> C e. R. )
34 ltpsrprg 7870 . . . . . . . . . . . . 13 |- ( ( v e. P. /\ w e. P. /\ C e. R. ) -> ( ( C +R [ <. v , 1P >. ] ~R ) <R ( C +R [ <. w , 1P >. ] ~R ) <-> v <P w ) )
3531, 32, 33, 34syl3anc 1249 . . . . . . . . . . . 12 |- ( ( ( ( ( ( ph /\ v e. P. ) /\ A. a e. B -. v <P a ) /\ y e. A ) /\ ( C +R [ <. v , 1P >. ] ~R ) <R y ) /\ ( w e. P. /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) ) -> ( ( C +R [ <. v , 1P >. ] ~R ) <R ( C +R [ <. w , 1P >. ] ~R ) <-> v <P w ) )
3630, 35mpbid 147 . . . . . . . . . . 11 |- ( ( ( ( ( ( ph /\ v e. P. ) /\ A. a e. B -. v <P a ) /\ y e. A ) /\ ( C +R [ <. v , 1P >. ] ~R ) <R y ) /\ ( w e. P. /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) ) -> v <P w )
37 equcom 1720 . . . . . . . . . . . . 13 |- ( w = a <-> a = w )
38 bicom 140 . . . . . . . . . . . . 13 |- ( ( -. v <P w <-> -. v <P a ) <-> ( -. v <P a <-> -. v <P w ) )
3917, 37, 383imtr3i 200 . . . . . . . . . . . 12 |- ( a = w -> ( -. v <P a <-> -. v <P w ) )
40 simp-4r 542 . . . . . . . . . . . 12 |- ( ( ( ( ( ( ph /\ v e. P. ) /\ A. a e. B -. v <P a ) /\ y e. A ) /\ ( C +R [ <. v , 1P >. ] ~R ) <R y ) /\ ( w e. P. /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) ) -> A. a e. B -. v <P a )
41 simpllr 534 . . . . . . . . . . . . . 14 |- ( ( ( ( ( ( ph /\ v e. P. ) /\ A. a e. B -. v <P a ) /\ y e. A ) /\ ( C +R [ <. v , 1P >. ] ~R ) <R y ) /\ ( w e. P. /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) ) -> y e. A )
4229, 41eqeltrd 2273 . . . . . . . . . . . . 13 |- ( ( ( ( ( ( ph /\ v e. P. ) /\ A. a e. B -. v <P a ) /\ y e. A ) /\ ( C +R [ <. v , 1P >. ] ~R ) <R y ) /\ ( w e. P. /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) ) -> ( C +R [ <. w , 1P >. ] ~R ) e. A )
431rabeq2i 2760 . . . . . . . . . . . . 13 |- ( w e. B <-> ( w e. P. /\ ( C +R [ <. w , 1P >. ] ~R ) e. A ) )
4432, 42, 43sylanbrc 417 . . . . . . . . . . . 12 |- ( ( ( ( ( ( ph /\ v e. P. ) /\ A. a e. B -. v <P a ) /\ y e. A ) /\ ( C +R [ <. v , 1P >. ] ~R ) <R y ) /\ ( w e. P. /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) ) -> w e. B )
4539, 40, 44rspcdva 2873 . . . . . . . . . . 11 |- ( ( ( ( ( ( ph /\ v e. P. ) /\ A. a e. B -. v <P a ) /\ y e. A ) /\ ( C +R [ <. v , 1P >. ] ~R ) <R y ) /\ ( w e. P. /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) ) -> -. v <P w )
4636, 45pm2.21fal 1384 . . . . . . . . . 10 |- ( ( ( ( ( ( ph /\ v e. P. ) /\ A. a e. B -. v <P a ) /\ y e. A ) /\ ( C +R [ <. v , 1P >. ] ~R ) <R y ) /\ ( w e. P. /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) ) -> F. )
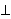4727, 46rexlimddv 2619 . . . . . . . . 9 |- ( ( ( ( ( ph /\ v e. P. ) /\ A. a e. B -. v <P a ) /\ y e. A ) /\ ( C +R [ <. v , 1P >. ] ~R ) <R y ) -> F. )
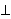4847inegd 1383 . . . . . . . 8 |- ( ( ( ( ph /\ v e. P. ) /\ A. a e. B -. v <P a ) /\ y e. A ) -> -. ( C +R [ <. v , 1P >. ] ~R ) <R y )
4948ralrimiva 2570 . . . . . . 7 |- ( ( ( ph /\ v e. P. ) /\ A. a e. B -. v <P a ) -> A. y e. A -. ( C +R [ <. v , 1P >. ] ~R ) <R y )
5049ex 115 . . . . . 6 |- ( ( ph /\ v e. P. ) -> ( A. a e. B -. v <P a -> A. y e. A -. ( C +R [ <. v , 1P >. ] ~R ) <R y ) )
5118, 50biimtrid 152 . . . . 5 |- ( ( ph /\ v e. P. ) -> ( A. w e. B -. v <P w -> A. y e. A -. ( C +R [ <. v , 1P >. ] ~R ) <R y ) )
52 nfv 1542 . . . . . . . . . . . . . 14 |- F/ w ( ph /\ v e. P. )
53 nfra1 2528 . . . . . . . . . . . . . 14 |- F/ w A. w e. P. ( w <P v -> E. u e. B w <P u )
5452, 53nfan 1579 . . . . . . . . . . . . 13 |- F/ w ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) )
55 nfv 1542 . . . . . . . . . . . . 13 |- F/ w y e. R.
5654, 55nfan 1579 . . . . . . . . . . . 12 |- F/ w ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. )
57 nfv 1542 . . . . . . . . . . . 12 |- F/ w y <R ( C +R [ <. v , 1P >. ] ~R )
5856, 57nfan 1579 . . . . . . . . . . 11 |- F/ w ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) )
59 nfv 1542 . . . . . . . . . . 11 |- F/ w ( C +R -1R ) <R y
6058, 59nfan 1579 . . . . . . . . . 10 |- F/ w ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y )
61 simp-6r 546 . . . . . . . . . . . . 13 |- ( ( ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) /\ w e. P. ) /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) -> A. w e. P. ( w <P v -> E. u e. B w <P u ) )
62 simplr 528 . . . . . . . . . . . . 13 |- ( ( ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) /\ w e. P. ) /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) -> w e. P. )
63 simpr 110 . . . . . . . . . . . . . . 15 |- ( ( ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) /\ w e. P. ) /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) -> ( C +R [ <. w , 1P >. ] ~R ) = y )
64 simp-4r 542 . . . . . . . . . . . . . . 15 |- ( ( ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) /\ w e. P. ) /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) -> y <R ( C +R [ <. v , 1P >. ] ~R ) )
6563, 64eqbrtrd 4055 . . . . . . . . . . . . . 14 |- ( ( ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) /\ w e. P. ) /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) -> ( C +R [ <. w , 1P >. ] ~R ) <R ( C +R [ <. v , 1P >. ] ~R ) )
66 simp-7r 548 . . . . . . . . . . . . . . 15 |- ( ( ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) /\ w e. P. ) /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) -> v e. P. )
679ad4antr 494 . . . . . . . . . . . . . . . 16 |- ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) -> C e. R. )
6867ad2antrr 488 . . . . . . . . . . . . . . 15 |- ( ( ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) /\ w e. P. ) /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) -> C e. R. )
69 ltpsrprg 7870 . . . . . . . . . . . . . . 15 |- ( ( w e. P. /\ v e. P. /\ C e. R. ) -> ( ( C +R [ <. w , 1P >. ] ~R ) <R ( C +R [ <. v , 1P >. ] ~R ) <-> w <P v ) )
7062, 66, 68, 69syl3anc 1249 . . . . . . . . . . . . . 14 |- ( ( ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) /\ w e. P. ) /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) -> ( ( C +R [ <. w , 1P >. ] ~R ) <R ( C +R [ <. v , 1P >. ] ~R ) <-> w <P v ) )
7165, 70mpbid 147 . . . . . . . . . . . . 13 |- ( ( ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) /\ w e. P. ) /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) -> w <P v )
72 rsp 2544 . . . . . . . . . . . . 13 |- ( A. w e. P. ( w <P v -> E. u e. B w <P u ) -> ( w e. P. -> ( w <P v -> E. u e. B w <P u ) ) )
7361, 62, 71, 72syl3c 63 . . . . . . . . . . . 12 |- ( ( ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) /\ w e. P. ) /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) -> E. u e. B w <P u )
74 breq2 4037 . . . . . . . . . . . . 13 |- ( u = b -> ( w <P u <-> w <P b ) )
7574cbvrexv 2730 . . . . . . . . . . . 12 |- ( E. u e. B w <P u <-> E. b e. B w <P b )
7673, 75sylib 122 . . . . . . . . . . 11 |- ( ( ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) /\ w e. P. ) /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) -> E. b e. B w <P b )
77 simprl 529 . . . . . . . . . . . . . 14 |- ( ( ( ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) /\ w e. P. ) /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) /\ ( b e. B /\ w <P b ) ) -> b e. B )
78 opeq1 3808 . . . . . . . . . . . . . . . . . 18 |- ( w = b -> <. w , 1P >. = <. b , 1P >. )
7978eceq1d 6628 . . . . . . . . . . . . . . . . 17 |- ( w = b -> [ <. w , 1P >. ] ~R = [ <. b , 1P >. ] ~R )
8079oveq2d 5938 . . . . . . . . . . . . . . . 16 |- ( w = b -> ( C +R [ <. w , 1P >. ] ~R ) = ( C +R [ <. b , 1P >. ] ~R ) )
8180eleq1d 2265 . . . . . . . . . . . . . . 15 |- ( w = b -> ( ( C +R [ <. w , 1P >. ] ~R ) e. A <-> ( C +R [ <. b , 1P >. ] ~R ) e. A ) )
8281, 1elrab2 2923 . . . . . . . . . . . . . 14 |- ( b e. B <-> ( b e. P. /\ ( C +R [ <. b , 1P >. ] ~R ) e. A ) )
8377, 82sylib 122 . . . . . . . . . . . . 13 |- ( ( ( ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) /\ w e. P. ) /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) /\ ( b e. B /\ w <P b ) ) -> ( b e. P. /\ ( C +R [ <. b , 1P >. ] ~R ) e. A ) )
8483simprd 114 . . . . . . . . . . . 12 |- ( ( ( ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) /\ w e. P. ) /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) /\ ( b e. B /\ w <P b ) ) -> ( C +R [ <. b , 1P >. ] ~R ) e. A )
85 simplr 528 . . . . . . . . . . . . 13 |- ( ( ( ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) /\ w e. P. ) /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) /\ ( b e. B /\ w <P b ) ) -> ( C +R [ <. w , 1P >. ] ~R ) = y )
86 simprr 531 . . . . . . . . . . . . . 14 |- ( ( ( ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) /\ w e. P. ) /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) /\ ( b e. B /\ w <P b ) ) -> w <P b )
87 simpllr 534 . . . . . . . . . . . . . . 15 |- ( ( ( ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) /\ w e. P. ) /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) /\ ( b e. B /\ w <P b ) ) -> w e. P. )
8883simpld 112 . . . . . . . . . . . . . . 15 |- ( ( ( ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) /\ w e. P. ) /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) /\ ( b e. B /\ w <P b ) ) -> b e. P. )
8967ad3antrrr 492 . . . . . . . . . . . . . . 15 |- ( ( ( ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) /\ w e. P. ) /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) /\ ( b e. B /\ w <P b ) ) -> C e. R. )
90 ltpsrprg 7870 . . . . . . . . . . . . . . 15 |- ( ( w e. P. /\ b e. P. /\ C e. R. ) -> ( ( C +R [ <. w , 1P >. ] ~R ) <R ( C +R [ <. b , 1P >. ] ~R ) <-> w <P b ) )
9187, 88, 89, 90syl3anc 1249 . . . . . . . . . . . . . 14 |- ( ( ( ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) /\ w e. P. ) /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) /\ ( b e. B /\ w <P b ) ) -> ( ( C +R [ <. w , 1P >. ] ~R ) <R ( C +R [ <. b , 1P >. ] ~R ) <-> w <P b ) )
9286, 91mpbird 167 . . . . . . . . . . . . 13 |- ( ( ( ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) /\ w e. P. ) /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) /\ ( b e. B /\ w <P b ) ) -> ( C +R [ <. w , 1P >. ] ~R ) <R ( C +R [ <. b , 1P >. ] ~R ) )
9385, 92eqbrtrrd 4057 . . . . . . . . . . . 12 |- ( ( ( ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) /\ w e. P. ) /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) /\ ( b e. B /\ w <P b ) ) -> y <R ( C +R [ <. b , 1P >. ] ~R ) )
94 breq2 4037 . . . . . . . . . . . . 13 |- ( z = ( C +R [ <. b , 1P >. ] ~R ) -> ( y <R z <-> y <R ( C +R [ <. b , 1P >. ] ~R ) ) )
9594rspcev 2868 . . . . . . . . . . . 12 |- ( ( ( C +R [ <. b , 1P >. ] ~R ) e. A /\ y <R ( C +R [ <. b , 1P >. ] ~R ) ) -> E. z e. A y <R z )
9684, 93, 95syl2anc 411 . . . . . . . . . . 11 |- ( ( ( ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) /\ w e. P. ) /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) /\ ( b e. B /\ w <P b ) ) -> E. z e. A y <R z )
9776, 96rexlimddv 2619 . . . . . . . . . 10 |- ( ( ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) /\ w e. P. ) /\ ( C +R [ <. w , 1P >. ] ~R ) = y ) -> E. z e. A y <R z )
98 simpr 110 . . . . . . . . . . 11 |- ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) -> ( C +R -1R ) <R y )
9967, 23syl 14 . . . . . . . . . . 11 |- ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) -> ( ( C +R -1R ) <R y <-> E. w e. P. ( C +R [ <. w , 1P >. ] ~R ) = y ) )
10098, 99mpbid 147 . . . . . . . . . 10 |- ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) -> E. w e. P. ( C +R [ <. w , 1P >. ] ~R ) = y )
10160, 97, 100r19.29af 2638 . . . . . . . . 9 |- ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ ( C +R -1R ) <R y ) -> E. z e. A y <R z )
1023ad5antr 496 . . . . . . . . . 10 |- ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ y <R C ) -> C e. A )
103 breq2 4037 . . . . . . . . . . 11 |- ( z = C -> ( y <R z <-> y <R C ) )
104103rspcev 2868 . . . . . . . . . 10 |- ( ( C e. A /\ y <R C ) -> E. z e. A y <R z )
105102, 104sylancom 420 . . . . . . . . 9 |- ( ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) /\ y <R C ) -> E. z e. A y <R z )
106 ltm1sr 7844 . . . . . . . . . . . 12 |- ( C e. R. -> ( C +R -1R ) <R C )
1078, 106syl 14 . . . . . . . . . . 11 |- ( ph -> ( C +R -1R ) <R C )
108107ad4antr 494 . . . . . . . . . 10 |- ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) -> ( C +R -1R ) <R C )
1099ad3antrrr 492 . . . . . . . . . . . 12 |- ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) -> C e. R. )
110 m1r 7819 . . . . . . . . . . . 12 |- -1R e. R.
111 addclsr 7820 . . . . . . . . . . . 12 |- ( ( C e. R. /\ -1R e. R. ) -> ( C +R -1R ) e. R. )
112109, 110, 111sylancl 413 . . . . . . . . . . 11 |- ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) -> ( C +R -1R ) e. R. )
113 simplr 528 . . . . . . . . . . 11 |- ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) -> y e. R. )
114 sowlin 4355 . . . . . . . . . . . 12 |- ( ( <R Or R. /\ ( ( C +R -1R ) e. R. /\ C e. R. /\ y e. R. ) ) -> ( ( C +R -1R ) <R C -> ( ( C +R -1R ) <R y \/ y <R C ) ) )
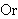
11519, 114mpan 424 . . . . . . . . . . 11 |- ( ( ( C +R -1R ) e. R. /\ C e. R. /\ y e. R. ) -> ( ( C +R -1R ) <R C -> ( ( C +R -1R ) <R y \/ y <R C ) ) )
116112, 109, 113, 115syl3anc 1249 . . . . . . . . . 10 |- ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) -> ( ( C +R -1R ) <R C -> ( ( C +R -1R ) <R y \/ y <R C ) ) )
117108, 116mpd 13 . . . . . . . . 9 |- ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) -> ( ( C +R -1R ) <R y \/ y <R C ) )
118101, 105, 117mpjaodan 799 . . . . . . . 8 |- ( ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) /\ y <R ( C +R [ <. v , 1P >. ] ~R ) ) -> E. z e. A y <R z )
119118ex 115 . . . . . . 7 |- ( ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) /\ y e. R. ) -> ( y <R ( C +R [ <. v , 1P >. ] ~R ) -> E. z e. A y <R z ) )
120119ralrimiva 2570 . . . . . 6 |- ( ( ( ph /\ v e. P. ) /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) -> A. y e. R. ( y <R ( C +R [ <. v , 1P >. ] ~R ) -> E. z e. A y <R z ) )
121120ex 115 . . . . 5 |- ( ( ph /\ v e. P. ) -> ( A. w e. P. ( w <P v -> E. u e. B w <P u ) -> A. y e. R. ( y <R ( C +R [ <. v , 1P >. ] ~R ) -> E. z e. A y <R z ) ) )
12251, 121anim12d 335 . . . 4 |- ( ( ph /\ v e. P. ) -> ( ( A. w e. B -. v <P w /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) -> ( A. y e. A -. ( C +R [ <. v , 1P >. ] ~R ) <R y /\ A. y e. R. ( y <R ( C +R [ <. v , 1P >. ] ~R ) -> E. z e. A y <R z ) ) ) )
123 breq1 4036 . . . . . . . 8 |- ( x = ( C +R [ <. v , 1P >. ] ~R ) -> ( x <R y <-> ( C +R [ <. v , 1P >. ] ~R ) <R y ) )
124123notbid 668 . . . . . . 7 |- ( x = ( C +R [ <. v , 1P >. ] ~R ) -> ( -. x <R y <-> -. ( C +R [ <. v , 1P >. ] ~R ) <R y ) )
125124ralbidv 2497 . . . . . 6 |- ( x = ( C +R [ <. v , 1P >. ] ~R ) -> ( A. y e. A -. x <R y <-> A. y e. A -. ( C +R [ <. v , 1P >. ] ~R ) <R y ) )
126 breq2 4037 . . . . . . . 8 |- ( x = ( C +R [ <. v , 1P >. ] ~R ) -> ( y <R x <-> y <R ( C +R [ <. v , 1P >. ] ~R ) ) )
127126imbi1d 231 . . . . . . 7 |- ( x = ( C +R [ <. v , 1P >. ] ~R ) -> ( ( y <R x -> E. z e. A y <R z ) <-> ( y <R ( C +R [ <. v , 1P >. ] ~R ) -> E. z e. A y <R z ) ) )
128127ralbidv 2497 . . . . . 6 |- ( x = ( C +R [ <. v , 1P >. ] ~R ) -> ( A. y e. R. ( y <R x -> E. z e. A y <R z ) <-> A. y e. R. ( y <R ( C +R [ <. v , 1P >. ] ~R ) -> E. z e. A y <R z ) ) )
129125, 128anbi12d 473 . . . . 5 |- ( x = ( C +R [ <. v , 1P >. ] ~R ) -> ( ( A. y e. A -. x <R y /\ A. y e. R. ( y <R x -> E. z e. A y <R z ) ) <-> ( A. y e. A -. ( C +R [ <. v , 1P >. ] ~R ) <R y /\ A. y e. R. ( y <R ( C +R [ <. v , 1P >. ] ~R ) -> E. z e. A y <R z ) ) ) )
130129rspcev 2868 . . . 4 |- ( ( ( C +R [ <. v , 1P >. ] ~R ) e. R. /\ ( A. y e. A -. ( C +R [ <. v , 1P >. ] ~R ) <R y /\ A. y e. R. ( y <R ( C +R [ <. v , 1P >. ] ~R ) -> E. z e. A y <R z ) ) ) -> E. x e. R. ( A. y e. A -. x <R y /\ A. y e. R. ( y <R x -> E. z e. A y <R z ) ) )
13115, 122, 130syl6an 1445 . . 3 |- ( ( ph /\ v e. P. ) -> ( ( A. w e. B -. v <P w /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) -> E. x e. R. ( A. y e. A -. x <R y /\ A. y e. R. ( y <R x -> E. z e. A y <R z ) ) ) )
132131rexlimdva 2614 . 2 |- ( ph -> ( E. v e. P. ( A. w e. B -. v <P w /\ A. w e. P. ( w <P v -> E. u e. B w <P u ) ) -> E. x e. R. ( A. y e. A -. x <R y /\ A. y e. R. ( y <R x -> E. z e. A y <R z ) ) ) )
1336, 132mpd 13 1 |- ( ph -> E. x e. R. ( A. y e. A -. x <R y /\ A. y e. R. ( y <R x -> E. z e. A y <R z ) ) )
Colors of variables: wff set class
Syntax hints:   -. wn 3   -> wi 4   /\ wa 104   <-> wb 105   \/ wo 709   /\ w3a 980   = wceq 1364   F. wfal 1369   e. wcel 2167   A.wral 2475   E.wrex 2476   {crab 2479   C_ wss 3157   <.cop 3625   class class class wbr 4033   Or wor 4330  (class class class)co 5922   [cec 6590   P.cnp 7358   1Pc1p 7359   <P cltp 7362   ~R cer 7363   R.cnr 7364   -1Rcm1r 7367   +R cplr 7368   <R cltr 7370
This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-ia1 106  ax-ia2 107  ax-ia3 108  ax-in1 615  ax-in2 616  ax-io 710  ax-5 1461  ax-7 1462  ax-gen 1463  ax-ie1 1507  ax-ie2 1508  ax-8 1518  ax-10 1519  ax-11 1520  ax-i12 1521  ax-bndl 1523  ax-4 1524  ax-17 1540  ax-i9 1544  ax-ial 1548  ax-i5r 1549  ax-13 2169  ax-14 2170  ax-ext 2178  ax-coll 4148  ax-sep 4151  ax-nul 4159  ax-pow 4207  ax-pr 4242  ax-un 4468  ax-setind 4573  ax-iinf 4624
This theorem depends on definitions:  df-bi 117  df-dc 836  df-3or 981  df-3an 982  df-tru 1367  df-fal 1370  df-nf 1475  df-sb 1777  df-eu 2048  df-mo 2049  df-clab 2183  df-cleq 2189  df-clel 2192  df-nfc 2328  df-ne 2368  df-ral 2480  df-rex 2481  df-reu 2482  df-rab 2484  df-v 2765  df-sbc 2990  df-csb 3085  df-dif 3159  df-un 3161  df-in 3163  df-ss 3170  df-nul 3451  df-pw 3607  df-sn 3628  df-pr 3629  df-op 3631  df-uni 3840  df-int 3875  df-iun 3918  df-br 4034  df-opab 4095  df-mpt 4096  df-tr 4132  df-eprel 4324  df-id 4328  df-po 4331  df-iso 4332  df-iord 4401  df-on 4403  df-suc 4406  df-iom 4627  df-xp 4669  df-rel 4670  df-cnv 4671  df-co 4672  df-dm 4673  df-rn 4674  df-res 4675  df-ima 4676  df-iota 5219  df-fun 5260  df-fn 5261  df-f 5262  df-f1 5263  df-fo 5264  df-f1o 5265  df-fv 5266  df-ov 5925  df-oprab 5926  df-mpo 5927  df-1st 6198  df-2nd 6199  df-recs 6363  df-irdg 6428  df-1o 6474  df-2o 6475  df-oadd 6478  df-omul 6479  df-er 6592  df-ec 6594  df-qs 6598  df-ni 7371  df-pli 7372  df-mi 7373  df-lti 7374  df-plpq 7411  df-mpq 7412  df-enq 7414  df-nqqs 7415  df-plqqs 7416  df-mqqs 7417  df-1nqqs 7418  df-rq 7419  df-ltnqqs 7420  df-enq0 7491  df-nq0 7492  df-0nq0 7493  df-plq0 7494  df-mq0 7495  df-inp 7533  df-i1p 7534  df-iplp 7535  df-imp 7536  df-iltp 7537  df-enr 7793  df-nr 7794  df-plr 7795  df-mr 7796  df-ltr 7797  df-0r 7798  df-1r 7799  df-m1r 7800
This theorem is referenced by:  suplocsr  7876
  Copyright terms: Public domain W3C validator