3dvds - Intuitionistic Logic Explorer

	Intuitionistic Logic Explorer		< Previous Next > Nearby theorems
Mirrors > Home > ILE Home > Th. List > 3dvds		Unicode version

Theorem 3dvds 12396

Description: A rule for divisibility by 3 of a number written in base 10. This is Metamath 100 proof #85. (Contributed by Mario Carneiro, 14-Jul-2014.) (Revised by Mario Carneiro, 17-Jan-2015.) (Revised by AV, 8-Sep-2021.)

**Assertion**
Ref	Expression
3dvds	$/\$ ;

Distinct variable groups:

Proof of Theorem 3dvds Dummy variable

is distinct from all other variables.

Step	Hyp	Ref	Expression
1		3z 9491	. . 3
2	1	a1i 9	. 2 $/\$
3		0zd 9474	. . . 4 $/\$
4		nn0z 9482	. . . . 5
5	4	adantr 276	. . . 4 $/\$
6	3, 5	fzfigd 10670	. . 3 $/\$
7		ffvelcdm 5773	. . . . 5 $/\$
8	7	adantll 476	. . . 4 $/\$ $/\$
9		10nn 9609	. . . . . 6 ;
10	9	nnzi 9483	. . . . 5 ;
11		elfznn0 10327	. . . . . 6
12	11	adantl 277	. . . . 5 $/\$ $/\$
13		zexpcl 10793	. . . . 5 ; $/\$ ;
14	10, 12, 13	sylancr 414	. . . 4 $/\$ $/\$ ;
15	8, 14	zmulcld 9591	. . 3 $/\$ $/\$ ;
16	6, 15	fsumzcl 11934	. 2 $/\$ ;
17	6, 8	fsumzcl 11934	. 2 $/\$
18	15, 8	zsubcld 9590	. . . 4 $/\$ $/\$ ;
19		ax-1cn 8108	. . . . . . . . . . . 12
20	9	nncni 9136	. . . . . . . . . . . 12 ;
21	19, 20	negsubdi2i 8448	. . . . . . . . . . 11 ; ;
22		9p1e10 9596	. . . . . . . . . . . . 13 ;
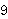23	22	eqcomi 2233	. . . . . . . . . . . 12 ;
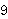24	23	oveq1i 6020	. . . . . . . . . . 11 ;
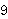25		9cn 9214	. . . . . . . . . . . 12
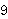26	25, 19	pncan3oi 8378	. . . . . . . . . . 11
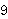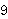27	21, 24, 26	3eqtri 2254	. . . . . . . . . 10 ;
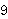28		3t3e9 9284	. . . . . . . . . 10
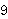29	27, 28	eqtr4i 2253	. . . . . . . . 9 ;
30	20	a1i 9	. . . . . . . . . . . . . . 15 ;
31		1re 8161	. . . . . . . . . . . . . . . . 17
32		10re 9612	. . . . . . . . . . . . . . . . 17 ;
33		1lt10 9732	. . . . . . . . . . . . . . . . 17 ;
34	31, 32, 33	gtapii 8797	. . . . . . . . . . . . . . . 16 ; #
35	34	a1i 9	. . . . . . . . . . . . . . 15 ; #
36		id 19	. . . . . . . . . . . . . . 15
37	30, 35, 36	geoserap 12039	. . . . . . . . . . . . . 14 ; ; ;
38		0zd 9474	. . . . . . . . . . . . . . . 16
39		nn0z 9482	. . . . . . . . . . . . . . . . 17
40		peano2zm 9500	. . . . . . . . . . . . . . . . 17
41	39, 40	syl 14	. . . . . . . . . . . . . . . 16
42	38, 41	fzfigd 10670	. . . . . . . . . . . . . . 15
43		elfznn0 10327	. . . . . . . . . . . . . . . . 17
44	43	adantl 277	. . . . . . . . . . . . . . . 16 $/\$
45		zexpcl 10793	. . . . . . . . . . . . . . . 16 ; $/\$ ;
46	10, 44, 45	sylancr 414	. . . . . . . . . . . . . . 15 $/\$ ;
47	42, 46	fsumzcl 11934	. . . . . . . . . . . . . 14 ;
48	37, 47	eqeltrrd 2307	. . . . . . . . . . . . 13 ; ;
49		1z 9488	. . . . . . . . . . . . . . 15
50		zsubcl 9503	. . . . . . . . . . . . . . 15 $/\$ ; ;
51	49, 10, 50	mp2an 426	. . . . . . . . . . . . . 14 ;
52	31, 33	ltneii 8259	. . . . . . . . . . . . . . 15 ;
53	19, 20	subeq0i 8442	. . . . . . . . . . . . . . . 16 ; ;
54	53	necon3bii 2438	. . . . . . . . . . . . . . 15 ; ;
55	52, 54	mpbir 146	. . . . . . . . . . . . . 14 ;
56	10, 36, 13	sylancr 414	. . . . . . . . . . . . . . 15 ;
57		zsubcl 9503	. . . . . . . . . . . . . . 15 $/\$ ; ;
58	49, 56, 57	sylancr 414	. . . . . . . . . . . . . 14 ;
59		dvdsval2 12322	. . . . . . . . . . . . . 14 ; $/\$ ; $/\$ ; ; ; ; ;
60	51, 55, 58, 59	mp3an12i 1375	. . . . . . . . . . . . 13 ; ; ; ;
61	48, 60	mpbird 167	. . . . . . . . . . . 12 ; ;
62	56	zcnd 9586	. . . . . . . . . . . . 13 ;
63		negsubdi2 8421	. . . . . . . . . . . . 13 ; $/\$ ; ;
64	62, 19, 63	sylancl 413	. . . . . . . . . . . 12 ; ;
65	61, 64	breqtrrd 4111	. . . . . . . . . . 11 ; ;
66		peano2zm 9500	. . . . . . . . . . . . 13 ; ;
67	56, 66	syl 14	. . . . . . . . . . . 12 ;
68		dvdsnegb 12340	. . . . . . . . . . . 12 ; $/\$ ; ; ; ; ;
69	51, 67, 68	sylancr 414	. . . . . . . . . . 11 ; ; ; ;
70	65, 69	mpbird 167	. . . . . . . . . 10 ; ;
71		negdvdsb 12339	. . . . . . . . . . 11 ; $/\$ ; ; ; ; ;
72	51, 67, 71	sylancr 414	. . . . . . . . . 10 ; ; ; ;
73	70, 72	mpbid 147	. . . . . . . . 9 ; ;
74	29, 73	eqbrtrrid 4119	. . . . . . . 8 ;
75		muldvds1 12348	. . . . . . . . 9 $/\$ $/\$ ; ; ;
76	1, 1, 67, 75	mp3an12i 1375	. . . . . . . 8 ; ;
77	74, 76	mpd 13	. . . . . . 7 ;
78	12, 77	syl 14	. . . . . 6 $/\$ $/\$ ;
79	14, 66	syl 14	. . . . . . 7 $/\$ $/\$ ;
80		dvdsmultr2 12365	. . . . . . 7 $/\$ $/\$ ; ; ;
81	1, 8, 79, 80	mp3an2i 1376	. . . . . 6 $/\$ $/\$ ; ;
82	78, 81	mpd 13	. . . . 5 $/\$ $/\$ ;
83	8	zcnd 9586	. . . . . 6 $/\$ $/\$
84	14	zcnd 9586	. . . . . 6 $/\$ $/\$ ;
85	83, 84	muls1d 8580	. . . . 5 $/\$ $/\$ ; ;
86	82, 85	breqtrd 4109	. . . 4 $/\$ $/\$ ;
87	6, 2, 18, 86	fsumdvds 12374	. . 3 $/\$ ;
88	15	zcnd 9586	. . . 4 $/\$ $/\$ ;
89	6, 88, 83	fsumsub 11984	. . 3 $/\$ ; ;
90	87, 89	breqtrd 4109	. 2 $/\$ ;
91		dvdssub2 12367	. 2 $/\$ ; $/\$ $/\$ ; ;
92	2, 16, 17, 90, 91	syl31anc 1274	1 $/\$ ;

Colors of variables: wff set class

Syntax hints:

wi 4 $/\$ wa 104

wb 105

wceq 1395

wcel 2200

wne 2400 class class class wbr 4083

wf 5317

cfv 5321 (class class class)co 6010

cc 8013

cc0 8015

c1 8016

caddc 8018

cmul 8020

cmin 8333

cneg 8334 # cap 8744

cdiv 8835

c3 9178

c9 9184

cn0 9385

cz 9462 ;cdc 9594

cfz 10221

cexp 10777

csu 11885

cdvds 12319

This theorem was proved from axioms: ax-mp 5 ax-1 6 ax-2 7 ax-ia1 106 ax-ia2 107 ax-ia3 108 ax-in1 617 ax-in2 618 ax-io 714 ax-5 1493 ax-7 1494 ax-gen 1495 ax-ie1 1539 ax-ie2 1540 ax-8 1550 ax-10 1551 ax-11 1552 ax-i12 1553 ax-bndl 1555 ax-4 1556 ax-17 1572 ax-i9 1576 ax-ial 1580 ax-i5r 1581 ax-13 2202 ax-14 2203 ax-ext 2211 ax-coll 4199 ax-sep 4202 ax-nul 4210 ax-pow 4259 ax-pr 4294 ax-un 4525 ax-setind 4630 ax-iinf 4681 ax-cnex 8106 ax-resscn 8107 ax-1cn 8108 ax-1re 8109 ax-icn 8110 ax-addcl 8111 ax-addrcl 8112 ax-mulcl 8113 ax-mulrcl 8114 ax-addcom 8115 ax-mulcom 8116 ax-addass 8117 ax-mulass 8118 ax-distr 8119 ax-i2m1 8120 ax-0lt1 8121 ax-1rid 8122 ax-0id 8123 ax-rnegex 8124 ax-precex 8125 ax-cnre 8126 ax-pre-ltirr 8127 ax-pre-ltwlin 8128 ax-pre-lttrn 8129 ax-pre-apti 8130 ax-pre-ltadd 8131 ax-pre-mulgt0 8132 ax-pre-mulext 8133 ax-arch 8134 ax-caucvg 8135

This theorem depends on definitions: df-bi 117 df-dc 840 df-3or 1003 df-3an 1004 df-tru 1398 df-fal 1401 df-nf 1507 df-sb 1809 df-eu 2080 df-mo 2081 df-clab 2216 df-cleq 2222 df-clel 2225 df-nfc 2361 df-ne 2401 df-nel 2496 df-ral 2513 df-rex 2514 df-reu 2515 df-rmo 2516 df-rab 2517 df-v 2801 df-sbc 3029 df-csb 3125 df-dif 3199 df-un 3201 df-in 3203 df-ss 3210 df-nul 3492 df-if 3603 df-pw 3651 df-sn 3672 df-pr 3673 df-op 3675 df-uni 3889 df-int 3924 df-iun 3967 df-br 4084 df-opab 4146 df-mpt 4147 df-tr 4183 df-id 4385 df-po 4388 df-iso 4389 df-iord 4458 df-on 4460 df-ilim 4461 df-suc 4463 df-iom 4684 df-xp 4726 df-rel 4727 df-cnv 4728 df-co 4729 df-dm 4730 df-rn 4731 df-res 4732 df-ima 4733 df-iota 5281 df-fun 5323 df-fn 5324 df-f 5325 df-f1 5326 df-fo 5327 df-f1o 5328 df-fv 5329 df-isom 5330 df-riota 5963 df-ov 6013 df-oprab 6014 df-mpo 6015 df-1st 6295 df-2nd 6296 df-recs 6462 df-irdg 6527 df-frec 6548 df-1o 6573 df-oadd 6577 df-er 6693 df-en 6901 df-dom 6902 df-fin 6903 df-pnf 8199 df-mnf 8200 df-xr 8201 df-ltxr 8202 df-le 8203 df-sub 8335 df-neg 8336 df-reap 8738 df-ap 8745 df-div 8836 df-inn 9127 df-2 9185 df-3 9186 df-4 9187 df-5 9188 df-6 9189 df-7 9190 df-8 9191 df-9 9192 df-n0 9386 df-z 9463 df-dec 9595 df-uz 9739 df-q 9832 df-rp 9867 df-fz 10222 df-fzo 10356 df-seqfrec 10687 df-exp 10778 df-ihash 11015 df-cj 11374 df-re 11375 df-im 11376 df-rsqrt 11530 df-abs 11531 df-clim 11811 df-sumdc 11886 df-dvds 12320

This theorem is referenced by: (None)

W3C validator