Theorem ltsonq 7596

Description: 'Less than' is a strict ordering on positive fractions. (Contributed by NM, 19-Feb-1996.) (Revised by Mario Carneiro, 4-May-2013.)

Assertion

Ref	Expression
ltsonq	|- <Q Or Q.

Proof of Theorem ltsonq

Dummy variables a b c d e f x y z w are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		df-nqqs 7546	. . . . . 6 |- Q. = ( ( N. X. N. ) /. ~Q )
2		id 19	. . . . . . . 8 |- ( [ <. z , w >. ] ~Q = x -> [ <. z , w >. ] ~Q = x )
3	2, 2	breq12d 4096	. . . . . . 7 |- ( [ <. z , w >. ] ~Q = x -> ( [ <. z , w >. ] ~Q <Q [ <. z , w >. ] ~Q <-> x <Q x ) )
4	3	notbid 671	. . . . . 6 |- ( [ <. z , w >. ] ~Q = x -> ( -. [ <. z , w >. ] ~Q <Q [ <. z , w >. ] ~Q <-> -. x <Q x ) )
5		ltsopi 7518	. . . . . . . 8 |- <N Or N.
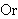6		ltrelpi 7522	. . . . . . . 8 |- <N C_ ( N. X. N. )
7	5, 6	soirri 5123	. . . . . . 7 |- -. ( w .N z ) <N ( w .N z )
8		ordpipqqs 7572	. . . . . . . . 9 |- ( ( ( z e. N. /\ w e. N. ) /\ ( z e. N. /\ w e. N. ) ) -> ( [ <. z , w >. ] ~Q <Q [ <. z , w >. ] ~Q <-> ( z .N w ) <N ( w .N z ) ) )
9	8	anidms 397	. . . . . . . 8 |- ( ( z e. N. /\ w e. N. ) -> ( [ <. z , w >. ] ~Q <Q [ <. z , w >. ] ~Q <-> ( z .N w ) <N ( w .N z ) ) )
10		mulcompig 7529	. . . . . . . . 9 |- ( ( z e. N. /\ w e. N. ) -> ( z .N w ) = ( w .N z ) )
11	10	breq1d 4093	. . . . . . . 8 |- ( ( z e. N. /\ w e. N. ) -> ( ( z .N w ) <N ( w .N z ) <-> ( w .N z ) <N ( w .N z ) ) )
12	9, 11	bitrd 188	. . . . . . 7 |- ( ( z e. N. /\ w e. N. ) -> ( [ <. z , w >. ] ~Q <Q [ <. z , w >. ] ~Q <-> ( w .N z ) <N ( w .N z ) ) )
13	7, 12	mtbiri 679	. . . . . 6 |- ( ( z e. N. /\ w e. N. ) -> -. [ <. z , w >. ] ~Q <Q [ <. z , w >. ] ~Q )
14	1, 4, 13	ecoptocl 6777	. . . . 5 |- ( x e. Q. -> -. x <Q x )
15	14	adantl 277	. . . 4 |- ( ( T. /\ x e. Q. ) -> -. x <Q x )
16		breq1 4086	. . . . . . . 8 |- ( [ <. a , b >. ] ~Q = x -> ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q <-> x <Q [ <. c , d >. ] ~Q ) )
17	16	anbi1d 465	. . . . . . 7 |- ( [ <. a , b >. ] ~Q = x -> ( ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) <-> ( x <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) ) )
18		breq1 4086	. . . . . . 7 |- ( [ <. a , b >. ] ~Q = x -> ( [ <. a , b >. ] ~Q <Q [ <. e , f >. ] ~Q <-> x <Q [ <. e , f >. ] ~Q ) )
19	17, 18	imbi12d 234	. . . . . 6 |- ( [ <. a , b >. ] ~Q = x -> ( ( ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) -> [ <. a , b >. ] ~Q <Q [ <. e , f >. ] ~Q ) <-> ( ( x <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) -> x <Q [ <. e , f >. ] ~Q ) ) )
20		breq2 4087	. . . . . . . 8 |- ( [ <. c , d >. ] ~Q = y -> ( x <Q [ <. c , d >. ] ~Q <-> x <Q y ) )
21		breq1 4086	. . . . . . . 8 |- ( [ <. c , d >. ] ~Q = y -> ( [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q <-> y <Q [ <. e , f >. ] ~Q ) )
22	20, 21	anbi12d 473	. . . . . . 7 |- ( [ <. c , d >. ] ~Q = y -> ( ( x <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) <-> ( x <Q y /\ y <Q [ <. e , f >. ] ~Q ) ) )
23	22	imbi1d 231	. . . . . 6 |- ( [ <. c , d >. ] ~Q = y -> ( ( ( x <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) -> x <Q [ <. e , f >. ] ~Q ) <-> ( ( x <Q y /\ y <Q [ <. e , f >. ] ~Q ) -> x <Q [ <. e , f >. ] ~Q ) ) )
24		breq2 4087	. . . . . . . 8 |- ( [ <. e , f >. ] ~Q = z -> ( y <Q [ <. e , f >. ] ~Q <-> y <Q z ) )
25	24	anbi2d 464	. . . . . . 7 |- ( [ <. e , f >. ] ~Q = z -> ( ( x <Q y /\ y <Q [ <. e , f >. ] ~Q ) <-> ( x <Q y /\ y <Q z ) ) )
26		breq2 4087	. . . . . . 7 |- ( [ <. e , f >. ] ~Q = z -> ( x <Q [ <. e , f >. ] ~Q <-> x <Q z ) )
27	25, 26	imbi12d 234	. . . . . 6 |- ( [ <. e , f >. ] ~Q = z -> ( ( ( x <Q y /\ y <Q [ <. e , f >. ] ~Q ) -> x <Q [ <. e , f >. ] ~Q ) <-> ( ( x <Q y /\ y <Q z ) -> x <Q z ) ) )
28		ordpipqqs 7572	. . . . . . . . . . . . . . . 16 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) ) -> ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q <-> ( a .N d ) <N ( b .N c ) ) )
29	28	3adant3 1041	. . . . . . . . . . . . . . 15 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q <-> ( a .N d ) <N ( b .N c ) ) )
30		simp1l 1045	. . . . . . . . . . . . . . . . 17 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> a e. N. )
31		simp2r 1048	. . . . . . . . . . . . . . . . 17 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> d e. N. )
32		mulclpi 7526	. . . . . . . . . . . . . . . . 17 |- ( ( a e. N. /\ d e. N. ) -> ( a .N d ) e. N. )
33	30, 31, 32	syl2anc 411	. . . . . . . . . . . . . . . 16 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( a .N d ) e. N. )
34		simp1r 1046	. . . . . . . . . . . . . . . . 17 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> b e. N. )
35		simp2l 1047	. . . . . . . . . . . . . . . . 17 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> c e. N. )
36		mulclpi 7526	. . . . . . . . . . . . . . . . 17 |- ( ( b e. N. /\ c e. N. ) -> ( b .N c ) e. N. )
37	34, 35, 36	syl2anc 411	. . . . . . . . . . . . . . . 16 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( b .N c ) e. N. )
38		simp3r 1050	. . . . . . . . . . . . . . . . 17 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> f e. N. )
39		mulclpi 7526	. . . . . . . . . . . . . . . . 17 |- ( ( c e. N. /\ f e. N. ) -> ( c .N f ) e. N. )
40	35, 38, 39	syl2anc 411	. . . . . . . . . . . . . . . 16 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( c .N f ) e. N. )
41		ltmpig 7537	. . . . . . . . . . . . . . . 16 |- ( ( ( a .N d ) e. N. /\ ( b .N c ) e. N. /\ ( c .N f ) e. N. ) -> ( ( a .N d ) <N ( b .N c ) <-> ( ( c .N f ) .N ( a .N d ) ) <N ( ( c .N f ) .N ( b .N c ) ) ) )
42	33, 37, 40, 41	syl3anc 1271	. . . . . . . . . . . . . . 15 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( ( a .N d ) <N ( b .N c ) <-> ( ( c .N f ) .N ( a .N d ) ) <N ( ( c .N f ) .N ( b .N c ) ) ) )
43	29, 42	bitrd 188	. . . . . . . . . . . . . 14 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q <-> ( ( c .N f ) .N ( a .N d ) ) <N ( ( c .N f ) .N ( b .N c ) ) ) )
44	43	biimpa 296	. . . . . . . . . . . . 13 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q ) -> ( ( c .N f ) .N ( a .N d ) ) <N ( ( c .N f ) .N ( b .N c ) ) )
45	44	adantrr 479	. . . . . . . . . . . 12 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) ) -> ( ( c .N f ) .N ( a .N d ) ) <N ( ( c .N f ) .N ( b .N c ) ) )
46		mulcompig 7529	. . . . . . . . . . . . . 14 |- ( ( ( c .N f ) e. N. /\ ( b .N c ) e. N. ) -> ( ( c .N f ) .N ( b .N c ) ) = ( ( b .N c ) .N ( c .N f ) ) )
47	40, 37, 46	syl2anc 411	. . . . . . . . . . . . 13 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( ( c .N f ) .N ( b .N c ) ) = ( ( b .N c ) .N ( c .N f ) ) )
48	47	adantr 276	. . . . . . . . . . . 12 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) ) -> ( ( c .N f ) .N ( b .N c ) ) = ( ( b .N c ) .N ( c .N f ) ) )
49	45, 48	breqtrd 4109	. . . . . . . . . . 11 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) ) -> ( ( c .N f ) .N ( a .N d ) ) <N ( ( b .N c ) .N ( c .N f ) ) )
50		ordpipqqs 7572	. . . . . . . . . . . . . . 15 |- ( ( ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q <-> ( c .N f ) <N ( d .N e ) ) )
51	50	3adant1 1039	. . . . . . . . . . . . . 14 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q <-> ( c .N f ) <N ( d .N e ) ) )
52		simp3l 1049	. . . . . . . . . . . . . . . 16 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> e e. N. )
53		mulclpi 7526	. . . . . . . . . . . . . . . 16 |- ( ( d e. N. /\ e e. N. ) -> ( d .N e ) e. N. )
54	31, 52, 53	syl2anc 411	. . . . . . . . . . . . . . 15 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( d .N e ) e. N. )
55		ltmpig 7537	. . . . . . . . . . . . . . 15 |- ( ( ( c .N f ) e. N. /\ ( d .N e ) e. N. /\ ( b .N c ) e. N. ) -> ( ( c .N f ) <N ( d .N e ) <-> ( ( b .N c ) .N ( c .N f ) ) <N ( ( b .N c ) .N ( d .N e ) ) ) )
56	40, 54, 37, 55	syl3anc 1271	. . . . . . . . . . . . . 14 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( ( c .N f ) <N ( d .N e ) <-> ( ( b .N c ) .N ( c .N f ) ) <N ( ( b .N c ) .N ( d .N e ) ) ) )
57	51, 56	bitrd 188	. . . . . . . . . . . . 13 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q <-> ( ( b .N c ) .N ( c .N f ) ) <N ( ( b .N c ) .N ( d .N e ) ) ) )
58	57	biimpa 296	. . . . . . . . . . . 12 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) -> ( ( b .N c ) .N ( c .N f ) ) <N ( ( b .N c ) .N ( d .N e ) ) )
59	58	adantrl 478	. . . . . . . . . . 11 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) ) -> ( ( b .N c ) .N ( c .N f ) ) <N ( ( b .N c ) .N ( d .N e ) ) )
60	5, 6	sotri 5124	. . . . . . . . . . 11 |- ( ( ( ( c .N f ) .N ( a .N d ) ) <N ( ( b .N c ) .N ( c .N f ) ) /\ ( ( b .N c ) .N ( c .N f ) ) <N ( ( b .N c ) .N ( d .N e ) ) ) -> ( ( c .N f ) .N ( a .N d ) ) <N ( ( b .N c ) .N ( d .N e ) ) )
61	49, 59, 60	syl2anc 411	. . . . . . . . . 10 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) ) -> ( ( c .N f ) .N ( a .N d ) ) <N ( ( b .N c ) .N ( d .N e ) ) )
62		mulcompig 7529	. . . . . . . . . . . . . . 15 |- ( ( x e. N. /\ y e. N. ) -> ( x .N y ) = ( y .N x ) )
63	62	adantl 277	. . . . . . . . . . . . . 14 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( x e. N. /\ y e. N. ) ) -> ( x .N y ) = ( y .N x ) )
64		mulasspig 7530	. . . . . . . . . . . . . . 15 |- ( ( x e. N. /\ y e. N. /\ z e. N. ) -> ( ( x .N y ) .N z ) = ( x .N ( y .N z ) ) )
65	64	adantl 277	. . . . . . . . . . . . . 14 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( x e. N. /\ y e. N. /\ z e. N. ) ) -> ( ( x .N y ) .N z ) = ( x .N ( y .N z ) ) )
66		mulclpi 7526	. . . . . . . . . . . . . . 15 |- ( ( x e. N. /\ y e. N. ) -> ( x .N y ) e. N. )
67	66	adantl 277	. . . . . . . . . . . . . 14 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( x e. N. /\ y e. N. ) ) -> ( x .N y ) e. N. )
68	35, 31, 30, 63, 65, 38, 67	caov411d 6197	. . . . . . . . . . . . 13 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( ( c .N d ) .N ( a .N f ) ) = ( ( a .N d ) .N ( c .N f ) ) )
69	63, 33, 40	caovcomd 6168	. . . . . . . . . . . . 13 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( ( a .N d ) .N ( c .N f ) ) = ( ( c .N f ) .N ( a .N d ) ) )
70	68, 69	eqtrd 2262	. . . . . . . . . . . 12 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( ( c .N d ) .N ( a .N f ) ) = ( ( c .N f ) .N ( a .N d ) ) )
71	35, 31, 34, 63, 65, 52, 67	caov4d 6196	. . . . . . . . . . . . 13 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( ( c .N d ) .N ( b .N e ) ) = ( ( c .N b ) .N ( d .N e ) ) )
72	63, 35, 34	caovcomd 6168	. . . . . . . . . . . . . 14 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( c .N b ) = ( b .N c ) )
73	72	oveq1d 6022	. . . . . . . . . . . . 13 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( ( c .N b ) .N ( d .N e ) ) = ( ( b .N c ) .N ( d .N e ) ) )
74	71, 73	eqtrd 2262	. . . . . . . . . . . 12 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( ( c .N d ) .N ( b .N e ) ) = ( ( b .N c ) .N ( d .N e ) ) )
75	70, 74	breq12d 4096	. . . . . . . . . . 11 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( ( ( c .N d ) .N ( a .N f ) ) <N ( ( c .N d ) .N ( b .N e ) ) <-> ( ( c .N f ) .N ( a .N d ) ) <N ( ( b .N c ) .N ( d .N e ) ) ) )
76	75	adantr 276	. . . . . . . . . 10 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) ) -> ( ( ( c .N d ) .N ( a .N f ) ) <N ( ( c .N d ) .N ( b .N e ) ) <-> ( ( c .N f ) .N ( a .N d ) ) <N ( ( b .N c ) .N ( d .N e ) ) ) )
77	61, 76	mpbird 167	. . . . . . . . 9 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) ) -> ( ( c .N d ) .N ( a .N f ) ) <N ( ( c .N d ) .N ( b .N e ) ) )
78		mulclpi 7526	. . . . . . . . . . . 12 |- ( ( a e. N. /\ f e. N. ) -> ( a .N f ) e. N. )
79	30, 38, 78	syl2anc 411	. . . . . . . . . . 11 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( a .N f ) e. N. )
80		mulclpi 7526	. . . . . . . . . . . 12 |- ( ( b e. N. /\ e e. N. ) -> ( b .N e ) e. N. )
81	34, 52, 80	syl2anc 411	. . . . . . . . . . 11 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( b .N e ) e. N. )
82		mulclpi 7526	. . . . . . . . . . . 12 |- ( ( c e. N. /\ d e. N. ) -> ( c .N d ) e. N. )
83	35, 31, 82	syl2anc 411	. . . . . . . . . . 11 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( c .N d ) e. N. )
84		ltmpig 7537	. . . . . . . . . . 11 |- ( ( ( a .N f ) e. N. /\ ( b .N e ) e. N. /\ ( c .N d ) e. N. ) -> ( ( a .N f ) <N ( b .N e ) <-> ( ( c .N d ) .N ( a .N f ) ) <N ( ( c .N d ) .N ( b .N e ) ) ) )
85	79, 81, 83, 84	syl3anc 1271	. . . . . . . . . 10 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( ( a .N f ) <N ( b .N e ) <-> ( ( c .N d ) .N ( a .N f ) ) <N ( ( c .N d ) .N ( b .N e ) ) ) )
86	85	adantr 276	. . . . . . . . 9 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) ) -> ( ( a .N f ) <N ( b .N e ) <-> ( ( c .N d ) .N ( a .N f ) ) <N ( ( c .N d ) .N ( b .N e ) ) ) )
87	77, 86	mpbird 167	. . . . . . . 8 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) ) -> ( a .N f ) <N ( b .N e ) )
88		ordpipqqs 7572	. . . . . . . . . 10 |- ( ( ( a e. N. /\ b e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( [ <. a , b >. ] ~Q <Q [ <. e , f >. ] ~Q <-> ( a .N f ) <N ( b .N e ) ) )
89	88	3adant2 1040	. . . . . . . . 9 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( [ <. a , b >. ] ~Q <Q [ <. e , f >. ] ~Q <-> ( a .N f ) <N ( b .N e ) ) )
90	89	adantr 276	. . . . . . . 8 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) ) -> ( [ <. a , b >. ] ~Q <Q [ <. e , f >. ] ~Q <-> ( a .N f ) <N ( b .N e ) ) )
91	87, 90	mpbird 167	. . . . . . 7 |- ( ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) /\ ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) ) -> [ <. a , b >. ] ~Q <Q [ <. e , f >. ] ~Q )
92	91	ex 115	. . . . . 6 |- ( ( ( a e. N. /\ b e. N. ) /\ ( c e. N. /\ d e. N. ) /\ ( e e. N. /\ f e. N. ) ) -> ( ( [ <. a , b >. ] ~Q <Q [ <. c , d >. ] ~Q /\ [ <. c , d >. ] ~Q <Q [ <. e , f >. ] ~Q ) -> [ <. a , b >. ] ~Q <Q [ <. e , f >. ] ~Q ) )
93	1, 19, 23, 27, 92	3ecoptocl 6779	. . . . 5 |- ( ( x e. Q. /\ y e. Q. /\ z e. Q. ) -> ( ( x <Q y /\ y <Q z ) -> x <Q z ) )
94	93	adantl 277	. . . 4 |- ( ( T. /\ ( x e. Q. /\ y e. Q. /\ z e. Q. ) ) -> ( ( x <Q y /\ y <Q z ) -> x <Q z ) )
95	15, 94	ispod 4395	. . 3 |- ( T. -> <Q Po Q. )
96		nqtri3or 7594	. . . 4 |- ( ( x e. Q. /\ y e. Q. ) -> ( x <Q y \/ x = y \/ y <Q x ) )
97	96	adantl 277	. . 3 |- ( ( T. /\ ( x e. Q. /\ y e. Q. ) ) -> ( x <Q y \/ x = y \/ y <Q x ) )
98	95, 97	issod 4410	. 2 |- ( T. -> <Q Or Q. )
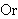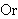99	98	mptru 1404	1 |- <Q Or Q.

Syntax hints:   -. wn 3   -> wi 4   /\ wa 104   <-> wb 105   \/ w3o 1001   /\ w3a 1002   = wceq 1395   T. wtru 1396   e. wcel 2200   <.cop 3669   class class class wbr 4083   Or wor 4386  (class class class)co 6007   [cec 6686   N.cnpi 7470   .N cmi 7472   <N clti 7473   ~Q ceq 7477   Q.cnq 7478   <Q cltq 7483

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-ia1 106  ax-ia2 107  ax-ia3 108  ax-in1 617  ax-in2 618  ax-io 714  ax-5 1493  ax-7 1494  ax-gen 1495  ax-ie1 1539  ax-ie2 1540  ax-8 1550  ax-10 1551  ax-11 1552  ax-i12 1553  ax-bndl 1555  ax-4 1556  ax-17 1572  ax-i9 1576  ax-ial 1580  ax-i5r 1581  ax-13 2202  ax-14 2203  ax-ext 2211  ax-coll 4199  ax-sep 4202  ax-nul 4210  ax-pow 4258  ax-pr 4293  ax-un 4524  ax-setind 4629  ax-iinf 4680

This theorem depends on definitions:  df-bi 117  df-dc 840  df-3or 1003  df-3an 1004  df-tru 1398  df-fal 1401  df-nf 1507  df-sb 1809  df-eu 2080  df-mo 2081  df-clab 2216  df-cleq 2222  df-clel 2225  df-nfc 2361  df-ne 2401  df-ral 2513  df-rex 2514  df-reu 2515  df-rab 2517  df-v 2801  df-sbc 3029  df-csb 3125  df-dif 3199  df-un 3201  df-in 3203  df-ss 3210  df-nul 3492  df-pw 3651  df-sn 3672  df-pr 3673  df-op 3675  df-uni 3889  df-int 3924  df-iun 3967  df-br 4084  df-opab 4146  df-mpt 4147  df-tr 4183  df-eprel 4380  df-id 4384  df-po 4387  df-iso 4388  df-iord 4457  df-on 4459  df-suc 4462  df-iom 4683  df-xp 4725  df-rel 4726  df-cnv 4727  df-co 4728  df-dm 4729  df-rn 4730  df-res 4731  df-ima 4732  df-iota 5278  df-fun 5320  df-fn 5321  df-f 5322  df-f1 5323  df-fo 5324  df-f1o 5325  df-fv 5326  df-ov 6010  df-oprab 6011  df-mpo 6012  df-1st 6292  df-2nd 6293  df-recs 6457  df-irdg 6522  df-oadd 6572  df-omul 6573  df-er 6688  df-ec 6690  df-qs 6694  df-ni 7502  df-mi 7504  df-lti 7505  df-enq 7545  df-nqqs 7546  df-ltnqqs 7551

This theorem is referenced by:  nqtric  7597  lt2addnq  7602  lt2mulnq  7603  ltbtwnnqq  7613  prarloclemarch2  7617  genplt2i  7708  genpdisj  7721  addlocprlemgt  7732  nqprdisj  7742  nqprloc  7743  addnqprlemfl  7757  addnqprlemfu  7758  prmuloclemcalc  7763  mulnqprlemfl  7773  mulnqprlemfu  7774  distrlem4prl  7782  distrlem4pru  7783  ltsopr  7794  ltexprlemopl  7799  ltexprlemopu  7801  ltexprlemdisj  7804  ltexprlemru  7810  recexprlemlol  7824  recexprlemupu  7826  recexprlemdisj  7828  recexprlemss1l  7833  recexprlemss1u  7834  cauappcvgprlemopl  7844  cauappcvgprlemlol  7845  cauappcvgprlemupu  7847  cauappcvgprlemdisj  7849  cauappcvgprlemloc  7850  cauappcvgprlemladdfu  7852  cauappcvgprlemladdru  7854  cauappcvgprlemladdrl  7855  caucvgprlemk  7863  caucvgprlemnkj  7864  caucvgprlemnbj  7865  caucvgprlemm  7866  caucvgprlemopl  7867  caucvgprlemlol  7868  caucvgprlemupu  7870  caucvgprlemloc  7873  caucvgprlemladdfu  7875  caucvgprprlemloccalc  7882  caucvgprprlemml  7892  caucvgprprlemopl  7895  suplocexprlemru  7917