Theorem pc2dvds 12848

Description: A characterization of divisibility in terms of prime count. (Contributed by Mario Carneiro, 23-Feb-2014.) (Revised by Mario Carneiro, 3-Oct-2014.)

Assertion

Ref	Expression
pc2dvds	|- ( ( A e. ZZ /\ B e. ZZ ) -> ( A || B <-> A. p e. Prime ( p pCnt A ) <_ ( p pCnt B ) ) )

Distinct variable groups:   A, p   B, p

Proof of Theorem pc2dvds

Step	Hyp	Ref	Expression
1		pcdvdstr 12845	. . . . 5 |- ( ( p e. Prime /\ ( A e. ZZ /\ B e. ZZ /\ A || B ) ) -> ( p pCnt A ) <_ ( p pCnt B ) )
2	1	ancoms 268	. . . 4 |- ( ( ( A e. ZZ /\ B e. ZZ /\ A || B ) /\ p e. Prime ) -> ( p pCnt A ) <_ ( p pCnt B ) )
3	2	ralrimiva 2603	. . 3 |- ( ( A e. ZZ /\ B e. ZZ /\ A || B ) -> A. p e. Prime ( p pCnt A ) <_ ( p pCnt B ) )
4	3	3expia 1229	. 2 |- ( ( A e. ZZ /\ B e. ZZ ) -> ( A || B -> A. p e. Prime ( p pCnt A ) <_ ( p pCnt B ) ) )
5		2prm 12644	. . . . . . . 8 |- 2 e. Prime
6		elex2 2816	. . . . . . . 8 |- ( 2 e. Prime -> E. w w e. Prime )
7	5, 6	ax-mp 5	. . . . . . 7 |- E. w w e. Prime
8		r19.2m 3578	. . . . . . 7 |- ( ( E. w w e. Prime /\ A. p e. Prime ( p pCnt 0 ) <_ ( p pCnt B ) ) -> E. p e. Prime ( p pCnt 0 ) <_ ( p pCnt B ) )
9	7, 8	mpan 424	. . . . . 6 |- ( A. p e. Prime ( p pCnt 0 ) <_ ( p pCnt B ) -> E. p e. Prime ( p pCnt 0 ) <_ ( p pCnt B ) )
10		id 19	. . . . . . . . . . . . 13 |- ( p e. Prime -> p e. Prime )
11		zq 9817	. . . . . . . . . . . . . 14 |- ( B e. ZZ -> B e. QQ )
12	11	adantl 277	. . . . . . . . . . . . 13 |- ( ( A e. ZZ /\ B e. ZZ ) -> B e. QQ )
13		pcxcl 12829	. . . . . . . . . . . . 13 |- ( ( p e. Prime /\ B e. QQ ) -> ( p pCnt B ) e. RR* )
14	10, 12, 13	syl2anr 290	. . . . . . . . . . . 12 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ p e. Prime ) -> ( p pCnt B ) e. RR* )
15		pnfge 9981	. . . . . . . . . . . 12 |- ( ( p pCnt B ) e. RR* -> ( p pCnt B ) <_ +oo )
16	14, 15	syl 14	. . . . . . . . . . 11 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ p e. Prime ) -> ( p pCnt B ) <_ +oo )
17	16	biantrurd 305	. . . . . . . . . 10 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ p e. Prime ) -> ( +oo <_ ( p pCnt B ) <-> ( ( p pCnt B ) <_ +oo /\ +oo <_ ( p pCnt B ) ) ) )
18		pc0 12822	. . . . . . . . . . . 12 |- ( p e. Prime -> ( p pCnt 0 ) = +oo )
19	18	adantl 277	. . . . . . . . . . 11 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ p e. Prime ) -> ( p pCnt 0 ) = +oo )
20	19	breq1d 4092	. . . . . . . . . 10 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ p e. Prime ) -> ( ( p pCnt 0 ) <_ ( p pCnt B ) <-> +oo <_ ( p pCnt B ) ) )
21		pnfxr 8195	. . . . . . . . . . 11 |- +oo e. RR*
22		xrletri3 9996	. . . . . . . . . . 11 |- ( ( ( p pCnt B ) e. RR* /\ +oo e. RR* ) -> ( ( p pCnt B ) = +oo <-> ( ( p pCnt B ) <_ +oo /\ +oo <_ ( p pCnt B ) ) ) )
23	14, 21, 22	sylancl 413	. . . . . . . . . 10 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ p e. Prime ) -> ( ( p pCnt B ) = +oo <-> ( ( p pCnt B ) <_ +oo /\ +oo <_ ( p pCnt B ) ) ) )
24	17, 20, 23	3bitr4d 220	. . . . . . . . 9 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ p e. Prime ) -> ( ( p pCnt 0 ) <_ ( p pCnt B ) <-> ( p pCnt B ) = +oo ) )
25		pnfnre 8184	. . . . . . . . . . . 12 |- +oo e/ RR
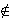26	25	neli 2497	. . . . . . . . . . 11 |- -. +oo e. RR
27		eleq1 2292	. . . . . . . . . . 11 |- ( ( p pCnt B ) = +oo -> ( ( p pCnt B ) e. RR <-> +oo e. RR ) )
28	26, 27	mtbiri 679	. . . . . . . . . 10 |- ( ( p pCnt B ) = +oo -> -. ( p pCnt B ) e. RR )
29		simplr 528	. . . . . . . . . . . 12 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ p e. Prime ) -> B e. ZZ )
30		0zd 9454	. . . . . . . . . . . 12 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ p e. Prime ) -> 0 e. ZZ )
31		zdceq 9518	. . . . . . . . . . . 12 |- ( ( B e. ZZ /\ 0 e. ZZ ) -> DECID B = 0 )
32	29, 30, 31	syl2anc 411	. . . . . . . . . . 11 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ p e. Prime ) -> DECID B = 0 )
33		pczcl 12816	. . . . . . . . . . . . . . . . 17 |- ( ( p e. Prime /\ ( B e. ZZ /\ B =/= 0 ) ) -> ( p pCnt B ) e. NN0 )
34	33	nn0red 9419	. . . . . . . . . . . . . . . 16 |- ( ( p e. Prime /\ ( B e. ZZ /\ B =/= 0 ) ) -> ( p pCnt B ) e. RR )
35	34	adantll 476	. . . . . . . . . . . . . . 15 |- ( ( ( A e. ZZ /\ p e. Prime ) /\ ( B e. ZZ /\ B =/= 0 ) ) -> ( p pCnt B ) e. RR )
36	35	an4s 590	. . . . . . . . . . . . . 14 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ ( p e. Prime /\ B =/= 0 ) ) -> ( p pCnt B ) e. RR )
37	36	expr 375	. . . . . . . . . . . . 13 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ p e. Prime ) -> ( B =/= 0 -> ( p pCnt B ) e. RR ) )
38	37	a1d 22	. . . . . . . . . . . 12 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ p e. Prime ) -> (DECID B = 0 -> ( B =/= 0 -> ( p pCnt B ) e. RR ) ) )
39	38	necon1bddc 2477	. . . . . . . . . . 11 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ p e. Prime ) -> (DECID B = 0 -> ( -. ( p pCnt B ) e. RR -> B = 0 ) ) )
40	32, 39	mpd 13	. . . . . . . . . 10 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ p e. Prime ) -> ( -. ( p pCnt B ) e. RR -> B = 0 ) )
41	28, 40	syl5 32	. . . . . . . . 9 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ p e. Prime ) -> ( ( p pCnt B ) = +oo -> B = 0 ) )
42	24, 41	sylbid 150	. . . . . . . 8 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ p e. Prime ) -> ( ( p pCnt 0 ) <_ ( p pCnt B ) -> B = 0 ) )
43	42	rexlimdva 2648	. . . . . . 7 |- ( ( A e. ZZ /\ B e. ZZ ) -> ( E. p e. Prime ( p pCnt 0 ) <_ ( p pCnt B ) -> B = 0 ) )
44		0dvds 12317	. . . . . . . 8 |- ( B e. ZZ -> ( 0 || B <-> B = 0 ) )
45	44	adantl 277	. . . . . . 7 |- ( ( A e. ZZ /\ B e. ZZ ) -> ( 0 || B <-> B = 0 ) )
46	43, 45	sylibrd 169	. . . . . 6 |- ( ( A e. ZZ /\ B e. ZZ ) -> ( E. p e. Prime ( p pCnt 0 ) <_ ( p pCnt B ) -> 0 || B ) )
47	9, 46	syl5 32	. . . . 5 |- ( ( A e. ZZ /\ B e. ZZ ) -> ( A. p e. Prime ( p pCnt 0 ) <_ ( p pCnt B ) -> 0 || B ) )
48	47	adantr 276	. . . 4 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A = 0 ) -> ( A. p e. Prime ( p pCnt 0 ) <_ ( p pCnt B ) -> 0 || B ) )
49		oveq2 6008	. . . . . . . 8 |- ( A = 0 -> ( p pCnt A ) = ( p pCnt 0 ) )
50	49	breq1d 4092	. . . . . . 7 |- ( A = 0 -> ( ( p pCnt A ) <_ ( p pCnt B ) <-> ( p pCnt 0 ) <_ ( p pCnt B ) ) )
51	50	ralbidv 2530	. . . . . 6 |- ( A = 0 -> ( A. p e. Prime ( p pCnt A ) <_ ( p pCnt B ) <-> A. p e. Prime ( p pCnt 0 ) <_ ( p pCnt B ) ) )
52		breq1 4085	. . . . . 6 |- ( A = 0 -> ( A || B <-> 0 || B ) )
53	51, 52	imbi12d 234	. . . . 5 |- ( A = 0 -> ( ( A. p e. Prime ( p pCnt A ) <_ ( p pCnt B ) -> A || B ) <-> ( A. p e. Prime ( p pCnt 0 ) <_ ( p pCnt B ) -> 0 || B ) ) )
54	53	adantl 277	. . . 4 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A = 0 ) -> ( ( A. p e. Prime ( p pCnt A ) <_ ( p pCnt B ) -> A || B ) <-> ( A. p e. Prime ( p pCnt 0 ) <_ ( p pCnt B ) -> 0 || B ) ) )
55	48, 54	mpbird 167	. . 3 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A = 0 ) -> ( A. p e. Prime ( p pCnt A ) <_ ( p pCnt B ) -> A || B ) )
56		zdvdsdc 12318	. . . . 5 |- ( ( A e. ZZ /\ B e. ZZ ) -> DECID A || B )
57	56	adantr 276	. . . 4 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> DECID A || B )
58		gcddvds 12479	. . . . . . . . . . . 12 |- ( ( A e. ZZ /\ B e. ZZ ) -> ( ( A gcd B ) || A /\ ( A gcd B ) || B ) )
59	58	simpld 112	. . . . . . . . . . 11 |- ( ( A e. ZZ /\ B e. ZZ ) -> ( A gcd B ) || A )
60		gcdcl 12482	. . . . . . . . . . . . 13 |- ( ( A e. ZZ /\ B e. ZZ ) -> ( A gcd B ) e. NN0 )
61	60	nn0zd 9563	. . . . . . . . . . . 12 |- ( ( A e. ZZ /\ B e. ZZ ) -> ( A gcd B ) e. ZZ )
62		simpl 109	. . . . . . . . . . . 12 |- ( ( A e. ZZ /\ B e. ZZ ) -> A e. ZZ )
63		dvdsabsb 12316	. . . . . . . . . . . 12 |- ( ( ( A gcd B ) e. ZZ /\ A e. ZZ ) -> ( ( A gcd B ) || A <-> ( A gcd B ) || ( abs ` A ) ) )
64	61, 62, 63	syl2anc 411	. . . . . . . . . . 11 |- ( ( A e. ZZ /\ B e. ZZ ) -> ( ( A gcd B ) || A <-> ( A gcd B ) || ( abs ` A ) ) )
65	59, 64	mpbid 147	. . . . . . . . . 10 |- ( ( A e. ZZ /\ B e. ZZ ) -> ( A gcd B ) || ( abs ` A ) )
66	65	adantr 276	. . . . . . . . 9 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( A gcd B ) || ( abs ` A ) )
67		simpl 109	. . . . . . . . . . . . 13 |- ( ( A = 0 /\ B = 0 ) -> A = 0 )
68	67	necon3ai 2449	. . . . . . . . . . . 12 |- ( A =/= 0 -> -. ( A = 0 /\ B = 0 ) )
69		gcdn0cl 12478	. . . . . . . . . . . 12 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ -. ( A = 0 /\ B = 0 ) ) -> ( A gcd B ) e. NN )
70	68, 69	sylan2 286	. . . . . . . . . . 11 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( A gcd B ) e. NN )
71	70	nnzd 9564	. . . . . . . . . 10 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( A gcd B ) e. ZZ )
72	70	nnne0d 9151	. . . . . . . . . 10 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( A gcd B ) =/= 0 )
73		nnabscl 11606	. . . . . . . . . . . 12 |- ( ( A e. ZZ /\ A =/= 0 ) -> ( abs ` A ) e. NN )
74	73	adantlr 477	. . . . . . . . . . 11 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( abs ` A ) e. NN )
75	74	nnzd 9564	. . . . . . . . . 10 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( abs ` A ) e. ZZ )
76		dvdsval2 12296	. . . . . . . . . 10 |- ( ( ( A gcd B ) e. ZZ /\ ( A gcd B ) =/= 0 /\ ( abs ` A ) e. ZZ ) -> ( ( A gcd B ) || ( abs ` A ) <-> ( ( abs ` A ) / ( A gcd B ) ) e. ZZ ) )
77	71, 72, 75, 76	syl3anc 1271	. . . . . . . . 9 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( ( A gcd B ) || ( abs ` A ) <-> ( ( abs ` A ) / ( A gcd B ) ) e. ZZ ) )
78	66, 77	mpbid 147	. . . . . . . 8 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( ( abs ` A ) / ( A gcd B ) ) e. ZZ )
79		nnre 9113	. . . . . . . . . . 11 |- ( ( abs ` A ) e. NN -> ( abs ` A ) e. RR )
80		nngt0 9131	. . . . . . . . . . 11 |- ( ( abs ` A ) e. NN -> 0 < ( abs ` A ) )
81	79, 80	jca 306	. . . . . . . . . 10 |- ( ( abs ` A ) e. NN -> ( ( abs ` A ) e. RR /\ 0 < ( abs ` A ) ) )
82		nnre 9113	. . . . . . . . . . 11 |- ( ( A gcd B ) e. NN -> ( A gcd B ) e. RR )
83		nngt0 9131	. . . . . . . . . . 11 |- ( ( A gcd B ) e. NN -> 0 < ( A gcd B ) )
84	82, 83	jca 306	. . . . . . . . . 10 |- ( ( A gcd B ) e. NN -> ( ( A gcd B ) e. RR /\ 0 < ( A gcd B ) ) )
85		divgt0 9015	. . . . . . . . . 10 |- ( ( ( ( abs ` A ) e. RR /\ 0 < ( abs ` A ) ) /\ ( ( A gcd B ) e. RR /\ 0 < ( A gcd B ) ) ) -> 0 < ( ( abs ` A ) / ( A gcd B ) ) )
86	81, 84, 85	syl2an 289	. . . . . . . . 9 |- ( ( ( abs ` A ) e. NN /\ ( A gcd B ) e. NN ) -> 0 < ( ( abs ` A ) / ( A gcd B ) ) )
87	74, 70, 86	syl2anc 411	. . . . . . . 8 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> 0 < ( ( abs ` A ) / ( A gcd B ) ) )
88		elnnz 9452	. . . . . . . 8 |- ( ( ( abs ` A ) / ( A gcd B ) ) e. NN <-> ( ( ( abs ` A ) / ( A gcd B ) ) e. ZZ /\ 0 < ( ( abs ` A ) / ( A gcd B ) ) ) )
89	78, 87, 88	sylanbrc 417	. . . . . . 7 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( ( abs ` A ) / ( A gcd B ) ) e. NN )
90		elnn1uz2 9798	. . . . . . 7 |- ( ( ( abs ` A ) / ( A gcd B ) ) e. NN <-> ( ( ( abs ` A ) / ( A gcd B ) ) = 1 \/ ( ( abs ` A ) / ( A gcd B ) ) e. ( ZZ>= ` 2 ) ) )
91	89, 90	sylib 122	. . . . . 6 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( ( ( abs ` A ) / ( A gcd B ) ) = 1 \/ ( ( abs ` A ) / ( A gcd B ) ) e. ( ZZ>= ` 2 ) ) )
92	58	simprd 114	. . . . . . . . . 10 |- ( ( A e. ZZ /\ B e. ZZ ) -> ( A gcd B ) || B )
93	92	adantr 276	. . . . . . . . 9 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( A gcd B ) || B )
94		breq1 4085	. . . . . . . . 9 |- ( ( A gcd B ) = ( abs ` A ) -> ( ( A gcd B ) || B <-> ( abs ` A ) || B ) )
95	93, 94	syl5ibcom 155	. . . . . . . 8 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( ( A gcd B ) = ( abs ` A ) -> ( abs ` A ) || B ) )
96	74	nncnd 9120	. . . . . . . . . 10 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( abs ` A ) e. CC )
97	70	nncnd 9120	. . . . . . . . . 10 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( A gcd B ) e. CC )
98		1cnd 8158	. . . . . . . . . 10 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> 1 e. CC )
99	70	nnap0d 9152	. . . . . . . . . 10 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( A gcd B ) # 0 )
100	96, 97, 98, 99	divmulapd 8955	. . . . . . . . 9 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( ( ( abs ` A ) / ( A gcd B ) ) = 1 <-> ( ( A gcd B ) x. 1 ) = ( abs ` A ) ) )
101	97	mulridd 8159	. . . . . . . . . 10 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( ( A gcd B ) x. 1 ) = ( A gcd B ) )
102	101	eqeq1d 2238	. . . . . . . . 9 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( ( ( A gcd B ) x. 1 ) = ( abs ` A ) <-> ( A gcd B ) = ( abs ` A ) ) )
103	100, 102	bitrd 188	. . . . . . . 8 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( ( ( abs ` A ) / ( A gcd B ) ) = 1 <-> ( A gcd B ) = ( abs ` A ) ) )
104		absdvdsb 12315	. . . . . . . . 9 |- ( ( A e. ZZ /\ B e. ZZ ) -> ( A || B <-> ( abs ` A ) || B ) )
105	104	adantr 276	. . . . . . . 8 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( A || B <-> ( abs ` A ) || B ) )
106	95, 103, 105	3imtr4d 203	. . . . . . 7 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( ( ( abs ` A ) / ( A gcd B ) ) = 1 -> A || B ) )
107		exprmfct 12655	. . . . . . . 8 |- ( ( ( abs ` A ) / ( A gcd B ) ) e. ( ZZ>= ` 2 ) -> E. p e. Prime p || ( ( abs ` A ) / ( A gcd B ) ) )
108		simprl 529	. . . . . . . . . . . . . . . 16 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> p e. Prime )
109	74	adantr 276	. . . . . . . . . . . . . . . . 17 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( abs ` A ) e. NN )
110	109	nnzd 9564	. . . . . . . . . . . . . . . 16 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( abs ` A ) e. ZZ )
111	109	nnne0d 9151	. . . . . . . . . . . . . . . 16 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( abs ` A ) =/= 0 )
112	70	adantr 276	. . . . . . . . . . . . . . . 16 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( A gcd B ) e. NN )
113		pcdiv 12820	. . . . . . . . . . . . . . . 16 |- ( ( p e. Prime /\ ( ( abs ` A ) e. ZZ /\ ( abs ` A ) =/= 0 ) /\ ( A gcd B ) e. NN ) -> ( p pCnt ( ( abs ` A ) / ( A gcd B ) ) ) = ( ( p pCnt ( abs ` A ) ) - ( p pCnt ( A gcd B ) ) ) )
114	108, 110, 111, 112, 113	syl121anc 1276	. . . . . . . . . . . . . . 15 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( p pCnt ( ( abs ` A ) / ( A gcd B ) ) ) = ( ( p pCnt ( abs ` A ) ) - ( p pCnt ( A gcd B ) ) ) )
115		simplll 533	. . . . . . . . . . . . . . . . . 18 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> A e. ZZ )
116		zq 9817	. . . . . . . . . . . . . . . . . 18 |- ( A e. ZZ -> A e. QQ )
117	115, 116	syl 14	. . . . . . . . . . . . . . . . 17 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> A e. QQ )
118		pcabs 12844	. . . . . . . . . . . . . . . . 17 |- ( ( p e. Prime /\ A e. QQ ) -> ( p pCnt ( abs ` A ) ) = ( p pCnt A ) )
119	108, 117, 118	syl2anc 411	. . . . . . . . . . . . . . . 16 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( p pCnt ( abs ` A ) ) = ( p pCnt A ) )
120	119	oveq1d 6015	. . . . . . . . . . . . . . 15 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( ( p pCnt ( abs ` A ) ) - ( p pCnt ( A gcd B ) ) ) = ( ( p pCnt A ) - ( p pCnt ( A gcd B ) ) ) )
121	114, 120	eqtrd 2262	. . . . . . . . . . . . . 14 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( p pCnt ( ( abs ` A ) / ( A gcd B ) ) ) = ( ( p pCnt A ) - ( p pCnt ( A gcd B ) ) ) )
122		simprr 531	. . . . . . . . . . . . . . 15 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> p || ( ( abs ` A ) / ( A gcd B ) ) )
123	89	adantr 276	. . . . . . . . . . . . . . . 16 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( ( abs ` A ) / ( A gcd B ) ) e. NN )
124		pcelnn 12839	. . . . . . . . . . . . . . . 16 |- ( ( p e. Prime /\ ( ( abs ` A ) / ( A gcd B ) ) e. NN ) -> ( ( p pCnt ( ( abs ` A ) / ( A gcd B ) ) ) e. NN <-> p || ( ( abs ` A ) / ( A gcd B ) ) ) )
125	108, 123, 124	syl2anc 411	. . . . . . . . . . . . . . 15 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( ( p pCnt ( ( abs ` A ) / ( A gcd B ) ) ) e. NN <-> p || ( ( abs ` A ) / ( A gcd B ) ) ) )
126	122, 125	mpbird 167	. . . . . . . . . . . . . 14 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( p pCnt ( ( abs ` A ) / ( A gcd B ) ) ) e. NN )
127	121, 126	eqeltrrd 2307	. . . . . . . . . . . . 13 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( ( p pCnt A ) - ( p pCnt ( A gcd B ) ) ) e. NN )
128	108, 112	pccld 12818	. . . . . . . . . . . . . . 15 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( p pCnt ( A gcd B ) ) e. NN0 )
129	128	nn0zd 9563	. . . . . . . . . . . . . 14 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( p pCnt ( A gcd B ) ) e. ZZ )
130		simplr 528	. . . . . . . . . . . . . . . 16 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> A =/= 0 )
131		pczcl 12816	. . . . . . . . . . . . . . . 16 |- ( ( p e. Prime /\ ( A e. ZZ /\ A =/= 0 ) ) -> ( p pCnt A ) e. NN0 )
132	108, 115, 130, 131	syl12anc 1269	. . . . . . . . . . . . . . 15 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( p pCnt A ) e. NN0 )
133	132	nn0zd 9563	. . . . . . . . . . . . . 14 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( p pCnt A ) e. ZZ )
134		znnsub 9494	. . . . . . . . . . . . . 14 |- ( ( ( p pCnt ( A gcd B ) ) e. ZZ /\ ( p pCnt A ) e. ZZ ) -> ( ( p pCnt ( A gcd B ) ) < ( p pCnt A ) <-> ( ( p pCnt A ) - ( p pCnt ( A gcd B ) ) ) e. NN ) )
135	129, 133, 134	syl2anc 411	. . . . . . . . . . . . 13 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( ( p pCnt ( A gcd B ) ) < ( p pCnt A ) <-> ( ( p pCnt A ) - ( p pCnt ( A gcd B ) ) ) e. NN ) )
136	127, 135	mpbird 167	. . . . . . . . . . . 12 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( p pCnt ( A gcd B ) ) < ( p pCnt A ) )
137		zltnle 9488	. . . . . . . . . . . . 13 |- ( ( ( p pCnt ( A gcd B ) ) e. ZZ /\ ( p pCnt A ) e. ZZ ) -> ( ( p pCnt ( A gcd B ) ) < ( p pCnt A ) <-> -. ( p pCnt A ) <_ ( p pCnt ( A gcd B ) ) ) )
138	129, 133, 137	syl2anc 411	. . . . . . . . . . . 12 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( ( p pCnt ( A gcd B ) ) < ( p pCnt A ) <-> -. ( p pCnt A ) <_ ( p pCnt ( A gcd B ) ) ) )
139	136, 138	mpbid 147	. . . . . . . . . . 11 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> -. ( p pCnt A ) <_ ( p pCnt ( A gcd B ) ) )
140	132	nn0red 9419	. . . . . . . . . . . . 13 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( p pCnt A ) e. RR )
141		simpllr 534	. . . . . . . . . . . . . . 15 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> B e. ZZ )
142		nprmdvds1 12657	. . . . . . . . . . . . . . . . . 18 |- ( p e. Prime -> -. p || 1 )
143	142	ad2antrl 490	. . . . . . . . . . . . . . . . 17 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> -. p || 1 )
144		gcdid0 12496	. . . . . . . . . . . . . . . . . . . . 21 |- ( A e. ZZ -> ( A gcd 0 ) = ( abs ` A ) )
145	115, 144	syl 14	. . . . . . . . . . . . . . . . . . . 20 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( A gcd 0 ) = ( abs ` A ) )
146	145	oveq2d 6016	. . . . . . . . . . . . . . . . . . 19 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( ( abs ` A ) / ( A gcd 0 ) ) = ( ( abs ` A ) / ( abs ` A ) ) )
147	96	adantr 276	. . . . . . . . . . . . . . . . . . . 20 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( abs ` A ) e. CC )
148	109	nnap0d 9152	. . . . . . . . . . . . . . . . . . . 20 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( abs ` A ) # 0 )
149	147, 148	dividapd 8929	. . . . . . . . . . . . . . . . . . 19 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( ( abs ` A ) / ( abs ` A ) ) = 1 )
150	146, 149	eqtrd 2262	. . . . . . . . . . . . . . . . . 18 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( ( abs ` A ) / ( A gcd 0 ) ) = 1 )
151	150	breq2d 4094	. . . . . . . . . . . . . . . . 17 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( p || ( ( abs ` A ) / ( A gcd 0 ) ) <-> p || 1 ) )
152	143, 151	mtbird 677	. . . . . . . . . . . . . . . 16 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> -. p || ( ( abs ` A ) / ( A gcd 0 ) ) )
153		oveq2 6008	. . . . . . . . . . . . . . . . . . . 20 |- ( B = 0 -> ( A gcd B ) = ( A gcd 0 ) )
154	153	oveq2d 6016	. . . . . . . . . . . . . . . . . . 19 |- ( B = 0 -> ( ( abs ` A ) / ( A gcd B ) ) = ( ( abs ` A ) / ( A gcd 0 ) ) )
155	154	breq2d 4094	. . . . . . . . . . . . . . . . . 18 |- ( B = 0 -> ( p || ( ( abs ` A ) / ( A gcd B ) ) <-> p || ( ( abs ` A ) / ( A gcd 0 ) ) ) )
156	122, 155	syl5ibcom 155	. . . . . . . . . . . . . . . . 17 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( B = 0 -> p || ( ( abs ` A ) / ( A gcd 0 ) ) ) )
157	156	necon3bd 2443	. . . . . . . . . . . . . . . 16 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( -. p || ( ( abs ` A ) / ( A gcd 0 ) ) -> B =/= 0 ) )
158	152, 157	mpd 13	. . . . . . . . . . . . . . 15 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> B =/= 0 )
159	108, 141, 158, 33	syl12anc 1269	. . . . . . . . . . . . . 14 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( p pCnt B ) e. NN0 )
160	159	nn0red 9419	. . . . . . . . . . . . 13 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( p pCnt B ) e. RR )
161		lemininf 11740	. . . . . . . . . . . . 13 |- ( ( ( p pCnt A ) e. RR /\ ( p pCnt A ) e. RR /\ ( p pCnt B ) e. RR ) -> ( ( p pCnt A ) <_ inf ( { ( p pCnt A ) , ( p pCnt B ) } , RR , < ) <-> ( ( p pCnt A ) <_ ( p pCnt A ) /\ ( p pCnt A ) <_ ( p pCnt B ) ) ) )
162	140, 140, 160, 161	syl3anc 1271	. . . . . . . . . . . 12 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( ( p pCnt A ) <_ inf ( { ( p pCnt A ) , ( p pCnt B ) } , RR , < ) <-> ( ( p pCnt A ) <_ ( p pCnt A ) /\ ( p pCnt A ) <_ ( p pCnt B ) ) ) )
163		pcgcd 12847	. . . . . . . . . . . . . . 15 |- ( ( p e. Prime /\ A e. ZZ /\ B e. ZZ ) -> ( p pCnt ( A gcd B ) ) = if ( ( p pCnt A ) <_ ( p pCnt B ) , ( p pCnt A ) , ( p pCnt B ) ) )
164	108, 115, 141, 163	syl3anc 1271	. . . . . . . . . . . . . 14 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( p pCnt ( A gcd B ) ) = if ( ( p pCnt A ) <_ ( p pCnt B ) , ( p pCnt A ) , ( p pCnt B ) ) )
165	159	nn0zd 9563	. . . . . . . . . . . . . . 15 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( p pCnt B ) e. ZZ )
166		2zinfmin 11749	. . . . . . . . . . . . . . 15 |- ( ( ( p pCnt A ) e. ZZ /\ ( p pCnt B ) e. ZZ ) -> inf ( { ( p pCnt A ) , ( p pCnt B ) } , RR , < ) = if ( ( p pCnt A ) <_ ( p pCnt B ) , ( p pCnt A ) , ( p pCnt B ) ) )
167	133, 165, 166	syl2anc 411	. . . . . . . . . . . . . 14 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> inf ( { ( p pCnt A ) , ( p pCnt B ) } , RR , < ) = if ( ( p pCnt A ) <_ ( p pCnt B ) , ( p pCnt A ) , ( p pCnt B ) ) )
168	164, 167	eqtr4d 2265	. . . . . . . . . . . . 13 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( p pCnt ( A gcd B ) ) = inf ( { ( p pCnt A ) , ( p pCnt B ) } , RR , < ) )
169	168	breq2d 4094	. . . . . . . . . . . 12 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( ( p pCnt A ) <_ ( p pCnt ( A gcd B ) ) <-> ( p pCnt A ) <_ inf ( { ( p pCnt A ) , ( p pCnt B ) } , RR , < ) ) )
170	140	leidd 8657	. . . . . . . . . . . . 13 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( p pCnt A ) <_ ( p pCnt A ) )
171	170	biantrurd 305	. . . . . . . . . . . 12 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( ( p pCnt A ) <_ ( p pCnt B ) <-> ( ( p pCnt A ) <_ ( p pCnt A ) /\ ( p pCnt A ) <_ ( p pCnt B ) ) ) )
172	162, 169, 171	3bitr4rd 221	. . . . . . . . . . 11 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> ( ( p pCnt A ) <_ ( p pCnt B ) <-> ( p pCnt A ) <_ ( p pCnt ( A gcd B ) ) ) )
173	139, 172	mtbird 677	. . . . . . . . . 10 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ ( p e. Prime /\ p || ( ( abs ` A ) / ( A gcd B ) ) ) ) -> -. ( p pCnt A ) <_ ( p pCnt B ) )
174	173	expr 375	. . . . . . . . 9 |- ( ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) /\ p e. Prime ) -> ( p || ( ( abs ` A ) / ( A gcd B ) ) -> -. ( p pCnt A ) <_ ( p pCnt B ) ) )
175	174	reximdva 2632	. . . . . . . 8 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( E. p e. Prime p || ( ( abs ` A ) / ( A gcd B ) ) -> E. p e. Prime -. ( p pCnt A ) <_ ( p pCnt B ) ) )
176		rexnalim 2519	. . . . . . . 8 |- ( E. p e. Prime -. ( p pCnt A ) <_ ( p pCnt B ) -> -. A. p e. Prime ( p pCnt A ) <_ ( p pCnt B ) )
177	107, 175, 176	syl56 34	. . . . . . 7 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( ( ( abs ` A ) / ( A gcd B ) ) e. ( ZZ>= ` 2 ) -> -. A. p e. Prime ( p pCnt A ) <_ ( p pCnt B ) ) )
178	106, 177	orim12d 791	. . . . . 6 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( ( ( ( abs ` A ) / ( A gcd B ) ) = 1 \/ ( ( abs ` A ) / ( A gcd B ) ) e. ( ZZ>= ` 2 ) ) -> ( A || B \/ -. A. p e. Prime ( p pCnt A ) <_ ( p pCnt B ) ) ) )
179	91, 178	mpd 13	. . . . 5 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( A || B \/ -. A. p e. Prime ( p pCnt A ) <_ ( p pCnt B ) ) )
180	179	ord 729	. . . 4 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( -. A || B -> -. A. p e. Prime ( p pCnt A ) <_ ( p pCnt B ) ) )
181		condc 858	. . . 4 |- (DECID A || B -> ( ( -. A || B -> -. A. p e. Prime ( p pCnt A ) <_ ( p pCnt B ) ) -> ( A. p e. Prime ( p pCnt A ) <_ ( p pCnt B ) -> A || B ) ) )
182	57, 180, 181	sylc 62	. . 3 |- ( ( ( A e. ZZ /\ B e. ZZ ) /\ A =/= 0 ) -> ( A. p e. Prime ( p pCnt A ) <_ ( p pCnt B ) -> A || B ) )
183		0zd 9454	. . . . 5 |- ( ( A e. ZZ /\ B e. ZZ ) -> 0 e. ZZ )
184		zdceq 9518	. . . . 5 |- ( ( A e. ZZ /\ 0 e. ZZ ) -> DECID A = 0 )
185	62, 183, 184	syl2anc 411	. . . 4 |- ( ( A e. ZZ /\ B e. ZZ ) -> DECID A = 0 )
186		dcne 2411	. . . 4 |- (DECID A = 0 <-> ( A = 0 \/ A =/= 0 ) )
187	185, 186	sylib 122	. . 3 |- ( ( A e. ZZ /\ B e. ZZ ) -> ( A = 0 \/ A =/= 0 ) )
188	55, 182, 187	mpjaodan 803	. 2 |- ( ( A e. ZZ /\ B e. ZZ ) -> ( A. p e. Prime ( p pCnt A ) <_ ( p pCnt B ) -> A || B ) )
189	4, 188	impbid 129	1 |- ( ( A e. ZZ /\ B e. ZZ ) -> ( A || B <-> A. p e. Prime ( p pCnt A ) <_ ( p pCnt B ) ) )

Syntax hints:   -. wn 3   -> wi 4   /\ wa 104   <-> wb 105   \/ wo 713  DECID wdc 839   /\ w3a 1002   = wceq 1395   E.wex 1538   e. wcel 2200   =/= wne 2400   A.wral 2508   E.wrex 2509   ifcif 3602   {cpr 3667   class class class wbr 4082   ` cfv 5317  (class class class)co 6000  infcinf 7146   CCcc 7993   RRcr 7994   0cc0 7995   1c1 7996   x. cmul 8000   +oocpnf 8174   RR*cxr 8176   < clt 8177   <_ cle 8178   - cmin 8313   / cdiv 8815   NNcn 9106   2c2 9157   NN0cn0 9365   ZZcz 9442   ZZ>=cuz 9718   QQcq 9810   abscabs 11503   || cdvds 12293   gcd cgcd 12469   Primecprime 12624   pCnt cpc 12802

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-ia1 106  ax-ia2 107  ax-ia3 108  ax-in1 617  ax-in2 618  ax-io 714  ax-5 1493  ax-7 1494  ax-gen 1495  ax-ie1 1539  ax-ie2 1540  ax-8 1550  ax-10 1551  ax-11 1552  ax-i12 1553  ax-bndl 1555  ax-4 1556  ax-17 1572  ax-i9 1576  ax-ial 1580  ax-i5r 1581  ax-13 2202  ax-14 2203  ax-ext 2211  ax-coll 4198  ax-sep 4201  ax-nul 4209  ax-pow 4257  ax-pr 4292  ax-un 4523  ax-setind 4628  ax-iinf 4679  ax-cnex 8086  ax-resscn 8087  ax-1cn 8088  ax-1re 8089  ax-icn 8090  ax-addcl 8091  ax-addrcl 8092  ax-mulcl 8093  ax-mulrcl 8094  ax-addcom 8095  ax-mulcom 8096  ax-addass 8097  ax-mulass 8098  ax-distr 8099  ax-i2m1 8100  ax-0lt1 8101  ax-1rid 8102  ax-0id 8103  ax-rnegex 8104  ax-precex 8105  ax-cnre 8106  ax-pre-ltirr 8107  ax-pre-ltwlin 8108  ax-pre-lttrn 8109  ax-pre-apti 8110  ax-pre-ltadd 8111  ax-pre-mulgt0 8112  ax-pre-mulext 8113  ax-arch 8114  ax-caucvg 8115

This theorem depends on definitions:  df-bi 117  df-stab 836  df-dc 840  df-3or 1003  df-3an 1004  df-tru 1398  df-fal 1401  df-nf 1507  df-sb 1809  df-eu 2080  df-mo 2081  df-clab 2216  df-cleq 2222  df-clel 2225  df-nfc 2361  df-ne 2401  df-nel 2496  df-ral 2513  df-rex 2514  df-reu 2515  df-rmo 2516  df-rab 2517  df-v 2801  df-sbc 3029  df-csb 3125  df-dif 3199  df-un 3201  df-in 3203  df-ss 3210  df-nul 3492  df-if 3603  df-pw 3651  df-sn 3672  df-pr 3673  df-op 3675  df-uni 3888  df-int 3923  df-iun 3966  df-br 4083  df-opab 4145  df-mpt 4146  df-tr 4182  df-id 4383  df-po 4386  df-iso 4387  df-iord 4456  df-on 4458  df-ilim 4459  df-suc 4461  df-iom 4682  df-xp 4724  df-rel 4725  df-cnv 4726  df-co 4727  df-dm 4728  df-rn 4729  df-res 4730  df-ima 4731  df-iota 5277  df-fun 5319  df-fn 5320  df-f 5321  df-f1 5322  df-fo 5323  df-f1o 5324  df-fv 5325  df-isom 5326  df-riota 5953  df-ov 6003  df-oprab 6004  df-mpo 6005  df-1st 6284  df-2nd 6285  df-recs 6449  df-frec 6535  df-1o 6560  df-2o 6561  df-er 6678  df-en 6886  df-sup 7147  df-inf 7148  df-pnf 8179  df-mnf 8180  df-xr 8181  df-ltxr 8182  df-le 8183  df-sub 8315  df-neg 8316  df-reap 8718  df-ap 8725  df-div 8816  df-inn 9107  df-2 9165  df-3 9166  df-4 9167  df-n0 9366  df-xnn0 9429  df-z 9443  df-uz 9719  df-q 9811  df-rp 9846  df-fz 10201  df-fzo 10335  df-fl 10485  df-mod 10540  df-seqfrec 10665  df-exp 10756  df-cj 11348  df-re 11349  df-im 11350  df-rsqrt 11504  df-abs 11505  df-dvds 12294  df-gcd 12470  df-prm 12625  df-pc 12803

This theorem is referenced by:  pc11  12849  pcz  12850  pcprmpw2  12851  pockthg  12875