| Step | Hyp | Ref
| Expression |
|---|
| 1 | | prmind.5 |
. 2
         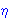   |
| 2 | | oveq2 6015 |
. . . 4
                  |
| 3 | 2 | raleqdv 2734 |
. . 3
        
                   |
| 4 | | oveq2 6015 |
. . . 4
                  |
| 5 | 4 | raleqdv 2734 |
. . 3
        
                   |
| 6 | | oveq2 6015 |
. . . 4
                          |
| 7 | 6 | raleqdv 2734 |
. . 3
            
                       |
| 8 | | oveq2 6015 |
. . . 4
                  |
| 9 | 8 | raleqdv 2734 |
. . 3
        
                   |
| 10 | | prmind.6 |
. . . . 5
  |
| 11 | | elfz1eq 10243 |
. . . . . 6
              |
| 12 | | prmind.1 |
. . . . . 6
            |
| 13 | 11, 12 | syl 14 |
. . . . 5
                |
| 14 | 10, 13 | mpbiri 168 |
. . . 4
            |
| 15 | 14 | rgen 2583 |
. . 3
          |
| 16 | | peano2nn 9133 |
. . . . . . . . . . . . 13
              |
| 17 | 16 | ad2antrr 488 |
. . . . . . . . . . . 12
                                                      |
| 18 | 17 | nncnd 9135 |
. . . . . . . . . . 11
                                                      |
| 19 | | elfzuz 10229 |
. . . . . . . . . . . . . 14
                          |
| 20 | 19 | ad2antrl 490 |
. . . . . . . . . . . . 13
                                                      |
| 21 | | eluz2nn 9773 |
. . . . . . . . . . . . 13
         
    |
| 22 | 20, 21 | syl 14 |
. . . . . . . . . . . 12
                                                  |
| 23 | 22 | nncnd 9135 |
. . . . . . . . . . 11
                                                  |
| 24 | 22 | nnap0d 9167 |
. . . . . . . . . . 11
                                               # #   |
| 25 | 18, 23, 24 | divcanap2d 8950 |
. . . . . . . . . 10
                                                                  |
| 26 | | simprr 531 |
. . . . . . . . . . . . 13
                                                      |
| 27 | 22 | nnzd 9579 |
. . . . . . . . . . . . . 14
                                                  |
| 28 | 22 | nnne0d 9166 |
. . . . . . . . . . . . . 14
                                                  |
| 29 | 17 | nnzd 9579 |
. . . . . . . . . . . . . 14
                                                      |
| 30 | | dvdsval2 12316 |
. . . . . . . . . . . . . 14
                                          |
| 31 | 27, 28, 29, 30 | syl3anc 1271 |
. . . . . . . . . . . . 13
                                                                    |
| 32 | 26, 31 | mpbid 147 |
. . . . . . . . . . . 12
                                                          |
| 33 | 23 | mulid2d 8176 |
. . . . . . . . . . . . . 14
                                                      |
| 34 | | elfzle2 10236 |
. . . . . . . . . . . . . . . . 17
                              |
| 35 | 34 | ad2antrl 490 |
. . . . . . . . . . . . . . . 16
                                                          |
| 36 | | nncn 9129 |
. . . . . . . . . . . . . . . . . 18
          |
| 37 | 36 | ad2antrr 488 |
. . . . . . . . . . . . . . . . 17
                                                  |
| 38 | | ax-1cn 8103 |
. . . . . . . . . . . . . . . . 17
    |
| 39 | | pncan 8363 |
. . . . . . . . . . . . . . . . 17
        
               |
| 40 | 37, 38, 39 | sylancl 413 |
. . . . . . . . . . . . . . . 16
                                                          |
| 41 | 35, 40 | breqtrd 4109 |
. . . . . . . . . . . . . . 15
                                                  |
| 42 | | nnz 9476 |
. . . . . . . . . . . . . . . . 17
          |
| 43 | 42 | ad2antrr 488 |
. . . . . . . . . . . . . . . 16
                                                  |
| 44 | | zleltp1 9513 |
. . . . . . . . . . . . . . . 16
        
                 |
| 45 | 27, 43, 44 | syl2anc 411 |
. . . . . . . . . . . . . . 15
                                                            |
| 46 | 41, 45 | mpbid 147 |
. . . . . . . . . . . . . 14
                                                      |
| 47 | 33, 46 | eqbrtrd 4105 |
. . . . . . . . . . . . 13
                                                          |
| 48 | | 1red 8172 |
. . . . . . . . . . . . . 14
                                                  |
| 49 | 17 | nnred 9134 |
. . . . . . . . . . . . . 14
                                                      |
| 50 | 22 | nnred 9134 |
. . . . . . . . . . . . . 14
                                                  |
| 51 | 22 | nngt0d 9165 |
. . . . . . . . . . . . . 14
                                                  |
| 52 | | ltmuldiv 9032 |
. . . . . . . . . . . . . 14
                         
            
             |
| 53 | 48, 49, 50, 51, 52 | syl112anc 1275 |
. . . . . . . . . . . . 13
                                                                        |
| 54 | 47, 53 | mpbid 147 |
. . . . . . . . . . . 12
                                                          |
| 55 | | eluz2b1 9808 |
. . . . . . . . . . . 12
                                            |
| 56 | 32, 54, 55 | sylanbrc 417 |
. . . . . . . . . . 11
                                                              |
| 57 | | prmind.2 |
. . . . . . . . . . . . 13
            |
| 58 | | simplr 528 |
. . . . . . . . . . . . 13
                                                        |
| 59 | | fznn 10297 |
. . . . . . . . . . . . . . 15
              
           |
| 60 | 43, 59 | syl 14 |
. . . . . . . . . . . . . 14
                                                                  |
| 61 | 22, 41, 60 | mpbir2and 950 |
. . . . . . . . . . . . 13
                                                      |
| 62 | 57, 58, 61 | rspcdva 2912 |
. . . . . . . . . . . 12
                                                |
| 63 | | vex 2802 |
. . . . . . . . . . . . . . 15
    |
| 64 | | prmind.3 |
. . . . . . . . . . . . . . 15
            |
| 65 | 63, 64 | sbcie 3063 |
. . . . . . . . . . . . . 14
      ![]. ].](_drbrack.gif)  
  |
| 66 | | dfsbcq 3030 |
. . . . . . . . . . . . . 14
                
  ![]. ].](_drbrack.gif)               ![]. ].](_drbrack.gif)    |
| 67 | 65, 66 | bitr3id 194 |
. . . . . . . . . . . . 13
                             ![]. ].](_drbrack.gif)    |
| 68 | 64 | cbvralv 2765 |
. . . . . . . . . . . . . 14
    
                 |
| 69 | 58, 68 | sylib 122 |
. . . . . . . . . . . . 13
                                                        |
| 70 | 17 | nnrpd 9902 |
. . . . . . . . . . . . . . . . 17
                                                      |
| 71 | 22 | nnrpd 9902 |
. . . . . . . . . . . . . . . . 17
                                                  |
| 72 | 70, 71 | rpdivcld 9922 |
. . . . . . . . . . . . . . . 16
                                                          |
| 73 | 72 | rpgt0d 9907 |
. . . . . . . . . . . . . . 15
                                                          |
| 74 | | elnnz 9467 |
. . . . . . . . . . . . . . 15
             
                          |
| 75 | 32, 73, 74 | sylanbrc 417 |
. . . . . . . . . . . . . 14
                                                          |
| 76 | 17 | nnap0d 9167 |
. . . . . . . . . . . . . . . . . 18
                                                   # #   |
| 77 | 18, 76 | dividapd 8944 |
. . . . . . . . . . . . . . . . 17
                                                              |
| 78 | | eluz2gt1 9809 |
. . . . . . . . . . . . . . . . . 18
         
    |
| 79 | 20, 78 | syl 14 |
. . . . . . . . . . . . . . . . 17
                                                  |
| 80 | 77, 79 | eqbrtrd 4105 |
. . . . . . . . . . . . . . . 16
                                                              |
| 81 | 17 | nngt0d 9165 |
. . . . . . . . . . . . . . . . 17
                                                      |
| 82 | | ltdiv23 9050 |
. . . . . . . . . . . . . . . . 17
                                                                          |
| 83 | 49, 49, 81, 50, 51, 82 | syl122anc 1280 |
. . . . . . . . . . . . . . . 16
                                                                                |
| 84 | 80, 83 | mpbid 147 |
. . . . . . . . . . . . . . 15
                                                              |
| 85 | | zleltp1 9513 |
. . . . . . . . . . . . . . . 16
                
                                 |
| 86 | 32, 43, 85 | syl2anc 411 |
. . . . . . . . . . . . . . 15
                                                                            |
| 87 | 84, 86 | mpbird 167 |
. . . . . . . . . . . . . 14
                                                          |
| 88 | | fznn 10297 |
. . . . . . . . . . . . . . 15
                      
                           |
| 89 | 43, 88 | syl 14 |
. . . . . . . . . . . . . 14
                                                                                          |
| 90 | 75, 87, 89 | mpbir2and 950 |
. . . . . . . . . . . . 13
                                                              |
| 91 | 67, 69, 90 | rspcdva 2912 |
. . . . . . . . . . . 12
                                                          ![]. ].](_drbrack.gif)   |
| 92 | 62, 91 | jca 306 |
. . . . . . . . . . 11
                                                             ![]. ].](_drbrack.gif)    |
| 93 | 67 | anbi2d 464 |
. . . . . . . . . . . . . 14
                                    ![]. ].](_drbrack.gif)     |
| 94 | | oveq2 6015 |
. . . . . . . . . . . . . . 15
                                  |
| 95 | 94 | sbceq1d 3033 |
. . . . . . . . . . . . . 14
                       ![]. ].](_drbrack.gif)                   ![]. ].](_drbrack.gif)    |
| 96 | 93, 95 | imbi12d 234 |
. . . . . . . . . . . . 13
                     
        ![]. ].](_drbrack.gif)   
                ![]. ].](_drbrack.gif)                    ![]. ].](_drbrack.gif)     |
| 97 | 96 | imbi2d 230 |
. . . . . . . . . . . 12
                              
        ![]. ].](_drbrack.gif)                              ![]. ].](_drbrack.gif)   
                ![]. ].](_drbrack.gif)      |
| 98 | | prmind2.8 |
. . . . . . . . . . . . . . 15
                   
          |
| 99 | 98 | ancoms 268 |
. . . . . . . . . . . . . 14
                   
          |
| 100 | | eluzelz 9743 |
. . . . . . . . . . . . . . . . 17
         
    |
| 101 | 100 | adantl 277 |
. . . . . . . . . . . . . . . 16
                   
    |
| 102 | | eluzelz 9743 |
. . . . . . . . . . . . . . . . 17
         
    |
| 103 | 102 | adantr 276 |
. . . . . . . . . . . . . . . 16
                   
    |
| 104 | 101, 103 | zmulcld 9586 |
. . . . . . . . . . . . . . 15
                   
        |
| 105 | | prmind.4 |
. . . . . . . . . . . . . . . 16
                |
| 106 | 105 | sbcieg 3061 |
. . . . . . . . . . . . . . 15
                   ![]. ].](_drbrack.gif)      |
| 107 | 104, 106 | syl 14 |
. . . . . . . . . . . . . 14
                   
         ![]. ].](_drbrack.gif)      |
| 108 | 99, 107 | sylibrd 169 |
. . . . . . . . . . . . 13
                   
               ![]. ].](_drbrack.gif)    |
| 109 | 108 | ex 115 |
. . . . . . . . . . . 12
         
               
        ![]. ].](_drbrack.gif)     |
| 110 | 97, 109 | vtoclga 2867 |
. . . . . . . . . . 11
                 
                         ![]. ].](_drbrack.gif)   
                ![]. ].](_drbrack.gif)     |
| 111 | 56, 20, 92, 110 | syl3c 63 |
. . . . . . . . . 10
                                                              ![]. ].](_drbrack.gif)   |
| 112 | 25, 111 | sbceq1dd 3034 |
. . . . . . . . 9
                                                      ![]. ].](_drbrack.gif)   |
| 113 | 112 | rexlimdvaa 2649 |
. . . . . . . 8
                                                   ![]. ].](_drbrack.gif)    |
| 114 | | ralnex 2518 |
. . . . . . . . 9
    
                     
                         |
| 115 | | simpl 109 |
. . . . . . . . . . . . . 14
                      |
| 116 | | elnnuz 9771 |
. . . . . . . . . . . . . 14
     
        |
| 117 | 115, 116 | sylib 122 |
. . . . . . . . . . . . 13
                          |
| 118 | | eluzp1p1 9760 |
. . . . . . . . . . . . 13
         
                |
| 119 | 117, 118 | syl 14 |
. . . . . . . . . . . 12
                                  |
| 120 | | df-2 9180 |
. . . . . . . . . . . . 13
        |
| 121 | 120 | fveq2i 5632 |
. . . . . . . . . . . 12
                |
| 122 | 119, 121 | eleqtrrdi 2323 |
. . . . . . . . . . 11
                              |
| 123 | | isprm3 12655 |
. . . . . . . . . . . 12
        
                                        |
| 124 | 123 | baibr 925 |
. . . . . . . . . . 11
             
   
                     
         |
| 125 | 122, 124 | syl 14 |
. . . . . . . . . 10
                                                     |
| 126 | | simpr 110 |
. . . . . . . . . . . . 13
                            |
| 127 | 57 | cbvralv 2765 |
. . . . . . . . . . . . 13
    
                 |
| 128 | 126, 127 | sylib 122 |
. . . . . . . . . . . 12
                            |
| 129 | 115 | nncnd 9135 |
. . . . . . . . . . . . . . 15
                      |
| 130 | 129, 38, 39 | sylancl 413 |
. . . . . . . . . . . . . 14
                              |
| 131 | 130 | oveq2d 6023 |
. . . . . . . . . . . . 13
                                      |
| 132 | 131 | raleqdv 2734 |
. . . . . . . . . . . 12
                                    
           |
| 133 | 128, 132 | mpbird 167 |
. . . . . . . . . . 11
                                    |
| 134 | | nfcv 2372 |
. . . . . . . . . . . 12
        |
| 135 | | nfv 1574 |
. . . . . . . . . . . . 13
    
               |
| 136 | | nfsbc1v 3047 |
. . . . . . . . . . . . 13
           ![]. ].](_drbrack.gif)  |
| 137 | 135, 136 | nfim 1618 |
. . . . . . . . . . . 12
                              ![]. ].](_drbrack.gif)   |
| 138 | | oveq1 6014 |
. . . . . . . . . . . . . . 15
                          |
| 139 | 138 | oveq2d 6023 |
. . . . . . . . . . . . . 14
                                  |
| 140 | 139 | raleqdv 2734 |
. . . . . . . . . . . . 13
            
                               |
| 141 | | sbceq1a 3038 |
. . . . . . . . . . . . 13
                     ![]. ].](_drbrack.gif)    |
| 142 | 140, 141 | imbi12d 234 |
. . . . . . . . . . . 12
                                               
        ![]. ].](_drbrack.gif)     |
| 143 | | prmind2.7 |
. . . . . . . . . . . . 13
         
           
  |
| 144 | 143 | ex 115 |
. . . . . . . . . . . 12
    
    
              |
| 145 | 134, 137,
142, 144 | vtoclgaf 2866 |
. . . . . . . . . . 11
        
    
                       ![]. ].](_drbrack.gif)    |
| 146 | 133, 145 | syl5com 29 |
. . . . . . . . . 10
                                   ![]. ].](_drbrack.gif)    |
| 147 | 125, 146 | sylbid 150 |
. . . . . . . . 9
                                           
        ![]. ].](_drbrack.gif)    |
| 148 | 114, 147 | biimtrrid 153 |
. . . . . . . 8
                      
                             ![]. ].](_drbrack.gif)    |
| 149 | | 2z 9485 |
. . . . . . . . . . 11
    |
| 150 | 149 | a1i 9 |
. . . . . . . . . 10
                      |
| 151 | 115 | nnzd 9579 |
. . . . . . . . . . . 12
                      |
| 152 | 151 | peano2zd 9583 |
. . . . . . . . . . 11
                          |
| 153 | | 1zzd 9484 |
. . . . . . . . . . 11
                      |
| 154 | 152, 153 | zsubcld 9585 |
. . . . . . . . . 10
                              |
| 155 | 19, 21 | syl 14 |
. . . . . . . . . . 11
                      |
| 156 | | dvdsdc 12324 |
. . . . . . . . . . 11
                DECID DECID  
      |
| 157 | 155, 152,
156 | syl2anr 290 |
. . . . . . . . . 10
                                    DECID
DECID 
       |
| 158 | 150, 154,
157 | exfzdc 10458 |
. . . . . . . . 9
                  DECID DECID  
                      |
| 159 | | exmiddc 841 |
. . . . . . . . 9
  DECID DECID                                                                            |
| 160 | 158, 159 | syl 14 |
. . . . . . . 8
                                                                     |
| 161 | 113, 148,
160 | mpjaod 723 |
. . . . . . 7
                          ![]. ].](_drbrack.gif)   |
| 162 | 161 | ex 115 |
. . . . . 6
        
                ![]. ].](_drbrack.gif)    |
| 163 | | ralsnsg 3703 |
. . . . . . 7
            
         
        ![]. ].](_drbrack.gif)    |
| 164 | 16, 163 | syl 14 |
. . . . . 6
        
         
        ![]. ].](_drbrack.gif)    |
| 165 | 162, 164 | sylibrd 169 |
. . . . 5
        
                     |
| 166 | 165 | ancld 325 |
. . . 4
        
                 
               |
| 167 | | fzsuc 10277 |
. . . . . . 7
         
                          |
| 168 | 116, 167 | sylbi 121 |
. . . . . 6
                                |
| 169 | 168 | raleqdv 2734 |
. . . . 5
        
                                 |
| 170 | | ralunb 3385 |
. . . . 5
    
                          
              |
| 171 | 169, 170 | bitrdi 196 |
. . . 4
        
                      
              |
| 172 | 166, 171 | sylibrd 169 |
. . 3
        
                       |
| 173 | 3, 5, 7, 9, 15, 172 | nnind 9137 |
. 2
                |
| 174 | | elfz1end 10263 |
. . 3
     
        |
| 175 | 174 | biimpi 120 |
. 2
              |
| 176 | 1, 173, 175 | rspcdva 2912 |
1
      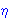  |